通过“30m折返跑”的测试成绩可以反映一个人的身体素质。在平直的跑道上,一学生站立在起点线处,当听到起跑口令后(测试员同时开始计时),跑向正前方30m处的折返线,到达折返线处时,用手触 摸固定在折返线处的标杆,再转身跑回起点线
摸固定在折返线处的标杆,再转身跑回起点线 ,返程无需减速,到达起点线处时,停止计时,全过程所用时间即为折返跑的成绩。学生可视为质点,加速或减速过程均视为匀变速,触摸杆的时间不计。该学生加
,返程无需减速,到达起点线处时,停止计时,全过程所用时间即为折返跑的成绩。学生可视为质点,加速或减速过程均视为匀变速,触摸杆的时间不计。该学生加 速时的加速度大小为a1=2.5m/s2,减速时的加速度大
速时的加速度大小为a1=2.5m/s2,减速时的加速度大 小为a2=5m/s2,到达折返线处时速度需减小到零,并且该生全过程中最大速度不超过Vm=12m/s。求该学生“30m折返跑”的最好成绩。
小为a2=5m/s2,到达折返线处时速度需减小到零,并且该生全过程中最大速度不超过Vm=12m/s。求该学生“30m折返跑”的最好成绩。
倾角为θ的斜面上有质量为m 的木块,它们之间的动摩擦因数为μ.现用水平力F推动木块,如图所示,使木块恰好沿斜面向上做匀速运动.若斜面始终保持静止,求水平推力F的大小.
.如图所示,套在足够长的绝缘粗糙直棒上的带正电小球,其质量为m,带电量为q,小球可在棒上滑动,小球与棒的动摩擦因数为μ,现将此棒竖直放入沿水平方向的且互相垂直的匀强磁场和匀强电场中,设小球电量不变,电场强度为E,磁感应强度为B,小球沿棒由静止开始下滑。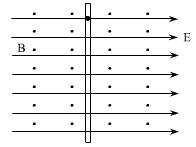
(1)试定性说明小球沿棒下滑的运动情况
(2)求小球下落的最大加速度
(3)求小球下落的最大速度
.如图所示,电源电动势ε=9V,内电阻r=0.5Ω,电阻R1=5.0Ω.R2=3.5Ω.R3=6.0Ω.R4=3.0Ω,电容C=2.0μF。求:
(1)当电键与a接触时电容带电量
(2)当电键与b接触时电容带电量
(3)当电键由与a接触转到与b接触时通过R3的电量
如图所示,电源电动势E=8V,内电阻为r=0.5Ω,“3V,3W”的灯泡L与电动机M串联接在电源上,灯泡刚好正常发光,电动机刚好正常工作,电动机的线圈电阻R0=1.5Ω。
求:(1)通过电动机的电流
(2)电源的输出功率
(3)电动机的输出功率
如图所示,水平绝缘光滑轨道AB的B端与处于竖直平面内的圆弧形光滑绝缘轨道BCD平滑连接,圆弧的半径R="0.50" m.轨道所在空间存在水平向右的匀强电场电场强度E=1.0×104 N/C.现有一质量m="0.06" kg的带电小球(可视为质点)放在水平轨道上与B端距离s="1.0" m 的位置,由于受到电场力的作用,带电体由静止开始运动.已知带电体所带的电荷量q=8.0×10-5 C,取g="10" m/s2,试问:
(1)带电小球能否到达圆弧最高点D?
(2)带电小球运动到何处时对轨道的压力最大?最大值为多少?