右下图为一示波管中的水平偏转极板,已知极板的长度为L,两板距离为d,所加偏转电压为U,且下板带正电;若一束电子以初速v0沿极板的中线进入偏转电场,最终电子从P点飞出。设电子的质量为m,电量为e ,不计电子的重力。试求电子在极板间运动的加速度大小;
电子通过极板发生的偏转距离y;
若规定图中的上极板电势为零,试求P点的电势。
如图所示,电阻R=0.1Ω的导体ab沿光滑的导线框向右做匀速运动,线框中接有电阻R=0.4Ω线框放在磁感应强度B=0.1T的匀强磁场中,磁场方向垂直于线框平面,导体ab的长度L=0.4m,运动速度v=5.0m/s.线框的电阻不计。
⑴电源的电动势(即产生的感应电动势)为多少?电路abcd中的电流为多少?
⑵求导体ab所受的安培力的大小,并判断其方向。
⑶外力做功的功率是多少?
如图所示,在光滑水平面上有一辆质量M="8" kg的平板小车,车上有一个质量m=1.9 kg的木块,木块距小车左端6m(木块可视为质点),车与木块一起以v="1" m/s的速度水平向右匀速行驶。一颗质量m0=0.1kg的子弹以v0="179" m/s的初.速度水平向左飞来,瞬间击中木块并留在其中。如果木块刚好不从车上掉下来,求木块与平板小车之间的动摩擦因数 。(g=l0m/s2)
。(g=l0m/s2)
由不同介质制成的两个半径均为R的透明四分之一圆柱体I和Ⅱ紧靠在一起,截面如图所示,圆心为0,顶部交点为D,以O为原点建立直角坐标系xOy。红色光束1从介质I底部的A( ,0)点垂直于界面入射;红色光束2平行于y轴向下射人介质Ⅱ,入射点为B且∠BOD=60°。已知透明介质I对红光的折射率
,0)点垂直于界面入射;红色光束2平行于y轴向下射人介质Ⅱ,入射点为B且∠BOD=60°。已知透明介质I对红光的折射率 ,透明介质Ⅱ对红光的折射率
,透明介质Ⅱ对红光的折射率 。设光束1经柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离为d。求:
。设光束1经柱面反射或折射后与y轴交点和光束2经柱体下底面折射后与y轴交点之间的距离为d。求:
①距离d的大小;
②若入射光换为蓝光,则距离d将比上面求得的结果大还是小?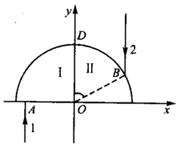
如图所示,两端开口的U形玻璃管两边粗细不同,粗管横截面积是细管的2倍。管中装入水银,两管中水银面与管口距离均为12 cm,大气压强为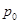 ="75" cmHg。现将粗管管口封闭,然后将细管管口用一活塞封闭并使活塞缓慢推入管中,直至两管中水银面高度差达6 cm为止。求活塞下移的距离。(环境温度不变)
="75" cmHg。现将粗管管口封闭,然后将细管管口用一活塞封闭并使活塞缓慢推入管中,直至两管中水银面高度差达6 cm为止。求活塞下移的距离。(环境温度不变)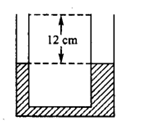
坐标原点O处有一放射源,它向xOy平面内的x轴下方各个方向发射速度大小都是v0的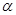 粒子,
粒子,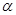 粒子的质量为m、电量为q;在0<y<d的区域内分布有指向y轴正方向的匀强电场,在y≥d的区域内分布有垂直于xOy平面向里的匀强磁场,磁感应强度B=
粒子的质量为m、电量为q;在0<y<d的区域内分布有指向y轴正方向的匀强电场,在y≥d的区域内分布有垂直于xOy平面向里的匀强磁场,磁感应强度B=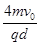 ,ab为一块很大的平面感光板,在磁场内平行于x轴放置,如图所示。测得进入磁场的a粒子的速率均为2v0,观察发现此时恰好无粒子打到ab板上。(
,ab为一块很大的平面感光板,在磁场内平行于x轴放置,如图所示。测得进入磁场的a粒子的速率均为2v0,观察发现此时恰好无粒子打到ab板上。(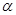 粒子的重力忽略不计)
粒子的重力忽略不计)
(1)求电场强度的大小;
(2)求感光板到x轴的距离;
(3)磁感应强度为多大时所有粒子均能打到板上?并求出此时ab板上被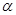 粒子打中的区域的长度。
粒子打中的区域的长度。