设抛物线y2＝8x的焦点为F，准线为
l，P为抛物线上一点，PA⊥l，
A为垂足．如果直线AF的斜率为－
，那么|PF|＝ ( )
| A．4 |
B．8 | C．8 |
D．16 |
如图所示，将一线圈放在匀强磁场中，线圈平面平行于磁感线，则线圈中有感应电流产生的是( )
| A．线圈绕N边转动 |
| B．线圈绕M边转动 |
| C．线圈垂直于磁感线向上运动 |
| D．线圈平行于磁感线的向右运动 |
如图所示，匀强磁场中有一通电直导线，关于导线受到的安培力F，下列判断不正确的是（）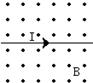
| A．F方向向上 | B．F大小与电流大小有关 |
| C．F大小与磁感应强度大小有关 | D．F大小与导线在磁场中的长度有关 |
一台理想变压器，原、副线圈的匝数比n1∶n2= 1∶4。原线圈接入220V交流电压，副线圈的电压为
| A．22V | B．55V | C．220V | D．880V |
如图所示，正点电荷外两点A、B处在以正点电荷为圆心的圆上。在A、B两点分别放上相同的带正电的试探电荷，关于试探电荷在两点的受力，下列判断正确的是( )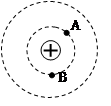
A.方向相同,且大小相等 B.方向相同,但大小不等
C.方向不同,但大小相等 D.方向与大小都不同
如图示是点电荷Q周围的电场线。将两个相同的试探电荷分别放在其中一根电场线上的A、B两点，不考虑试探电荷间的相互作用，下列说法正确的是（）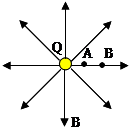
A. 电荷Q的电场为匀强电场
B. 电荷Q带负电
C. 试探电荷在A、B两点受力大小相等
D. 试探电荷在A点受力大于在B点受力