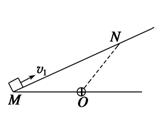
如图所示，粗糙程度均匀的绝缘斜面下方O点处有一正点电荷，带负电的小物体以初速度v1从M点沿斜面上滑，到达N点时速度为零，然后下滑回到M点，此时速度v2(v2＜v1)．若小物体电荷量保持不变，OM＝ON，则( )
| A．小物体上升的最大高度为 | B．从N到M的过程中，小物体的电势能逐渐减小 |
| C．从M到N的过程中，电场力对小物体先做负功后做正功 | |
| D．从N到M的过程中，小物体受到的摩擦力和电场力均是先增大后减小 |
下面给出的物理量中，哪一个物理量是矢量： （）
| A．位移； | B．加速度； | C．路程； | D．速率。 |
如图所示，小球从竖直砖墙某位置静止释放，用频闪照相机在同一底片上多次曝光，得到了图中1、2、3、4、5…所示小球运动过程中每次曝光的位置．连续两次曝光的时间间隔均为T，每块砖的厚度为d。根据图中的信息，下列判断错误的是 ( )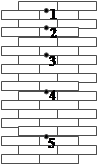
| A．位置“1”是小球释放的初始位置 |
| B．小球做匀加速直线运动 |
C．小球下落的加速度为 |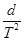
D．小球在位置“3”的速度为 |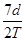
如图所示，一小球从A点由静止开始沿斜面做匀变速直线运动，若到达B点时速度为v，到达C点时速度为2v，则AB:BC等于 （ ）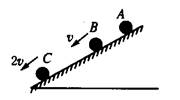
| A．1∶1 | B．1∶2 |
| C．1∶3 | D．1∶4 |
一汽车在平直的公路上以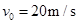
做匀速直线运动，刹车后，汽车以大小为
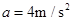的加速度做匀减速直线运动，那么刹车后经8s汽车通过的位移为（）
| A．50 m | B．32 m |
| C．288 m | D．以上答案都不对 |
如图是一辆汽车做直线运动的s-t图像，对线段OA、AB、BC、CD所表示的运动，下列说法正确的是 ( )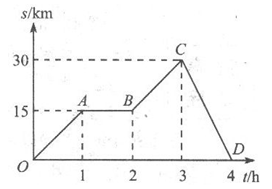
A．OA段运动速度最大
B．AB段物体做匀速运动
C．CD段的运动方向与初始运动方向相反
D．运动4h汽车的位移大小为30km