如图所示,在倾角为θ的光滑斜面上有两个用轻质弹簧 相连接的物块A 、B .它们的质量分别为mA、mB,弹簧的劲度
相连接的物块A 、B .它们的质量分别为mA、mB,弹簧的劲度 系数为k , C为一固定挡板。系统处于静止状态。现开始用一恒力F沿斜面方向拉物块A 使之向上运动,求物块B 刚要离开C时物块A 的加速度a 和从开始到此时物块A 的位移d。重力加速度为g。
系数为k , C为一固定挡板。系统处于静止状态。现开始用一恒力F沿斜面方向拉物块A 使之向上运动,求物块B 刚要离开C时物块A 的加速度a 和从开始到此时物块A 的位移d。重力加速度为g。
如图所示,传送带的水平部分ab=4m,斜面部分bc=4m,bc与水平面的夹角α=37°.一个小物体A与传送带的动摩擦因数μ=0.25,传送带沿图示的方向运动,速率v=2 m/s.若把物体A轻放到a处,它将被传送带送到c点,且物体A不会脱离传送带.求物体A从a点被传送到c点所用的时间.(已知:sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,物体的质量为5kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,求拉力F的大小范围.
如图所示,绝缘光滑轨道AB部分为倾角为30°的斜面,AC部分为竖直平面上半径为R的圆轨道,斜面与圆轨道相切.整个装置处于场强为E、方向水平向右的匀强电场中.现有一个质量为m的小球,带正电荷量为q=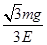 ,要使小球能安全通过圆轨道,在O点的初速度应满足什么条件?
,要使小球能安全通过圆轨道,在O点的初速度应满足什么条件?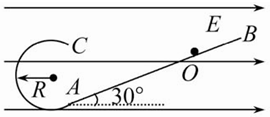
如图,一质量为m、电荷量为q(q>0)的粒子在匀强电场中运动,A、B为其运动轨迹上的两点。已知该粒子在A点的速度大小为v0,方向与电场方向的夹角为60°;它运动到B点时速度方向与电场方向的夹角为30°。不计重力。求A、B两点间的电势差。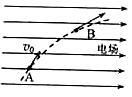
如图所示,在真空中的O点放一点电荷Q=1.0×10-9 C,直线MN过O点,OM="30" cm,M点放一点电荷q=-2×10-10 C,求: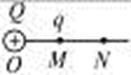
(1)M点的场强大小;
(2)若M点的电势比N点的电势高15 V,则电荷q从M点移到N点,它的电势能变化了多少?