(本题满分12分)已知AB是⊙O的一条弦,CD是⊙O的直径,CD⊥AB,垂足为K.现取一块三角板,把它的一个锐角顶点固定在点C处,该锐角的两边(从左到右)与直线AB和圆分别相交于E、F和G、H.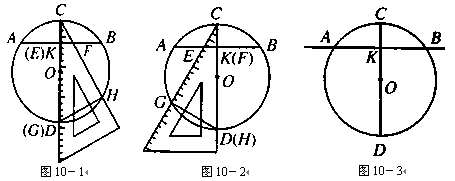
(1) 若∠C的一边过圆心,请选择图10-1或图10-2所示,求证: △CEF∽△CHG;
(2) 若∠C的边不过圆心,在图10-3中补全一种示意图,请你观察所画的图形,并判断(1)中的结论是否仍然成立?若成立,给予证明;若不成立,请说明理由.
如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=40m,某人在河岸MN的A处测得∠DAN=35°,然后沿河岸走了100m到达B处,测得∠CBN=70°.求河流的宽度CE(精确到1m).
(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70;sin 70°≈0.94,cos70°≈0.34,tan70°≈2.75).
“PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物,它造成的雾霾天气对人体健康的危害甚至要比沙尘暴更大.环境检测中心在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5检测,某日随机抽取25个监测点的研究性数据,并绘制成统计表和扇形统计图如下:
| 类别 |
组别 |
PM2.5日平均浓度值m (微克/立方米) |
频数 |
频率 |
| A |
1 |
15 m<30 m<30 |
2 |
0.08 |
| 2 |
30 m<45 m<45 |
3 |
0.12 |
|
| B |
3 |
45 m<60 m<60 |
a |
b |
| 4 |
60 m<75 m<75 |
5 |
0.20 |
|
| C |
5 |
75 m<90 m<90 |
6 |
c |
| D |
6 |
90 m<105 m<105 |
4 |
0.16 |
| 合计 |
以上分组均含最小值,不含最大值 |
25 |
1.00 |

根据图表中提供的信息解答下列问题:
(1)统计表中的a= ,b=,c=;
(2)在扇形统计图中,A类所对应的圆心角是度;
(3)我国PM2.5安全值的标准采用世卫组织(WHO)设定的最宽限值:日平均浓度小于75微克/立方米.请你估计当日环保监测中心在检测100个城市中,PM2.5日平均浓度值符合安全值的城市约有多少个?
如图,电路上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光.
(1)任意闭合其中一个开关,则小灯泡发光的概率等于 .
(2)任意闭合其中两个开关,请用画树状图或列表的方法求出小灯泡发光的概率.
在如图的方格纸中,每个小方格都是边长为1个单位的正方形,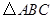 的三个顶点都在格点上(每个小方格的顶点叫格点).
的三个顶点都在格点上(每个小方格的顶点叫格点).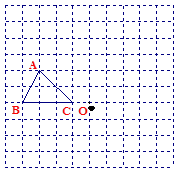
⑴ 画出△ABC关于点O的中心对称的△A1B1C1;
⑵ 如果建立平面直角坐标系,使点B的坐标为(-5,2),点C的坐标为(-2,2),则点A1的坐标为;
⑶ 将△ABC绕点O顺时针旋转90°,画出旋转后的△A2B2C2,并求线段BC扫过的面积.
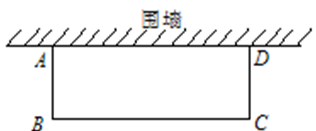
如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,则AB的长度是m(可利用的围墙长度超过6m).