(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线
 ,已知过点
,已知过点 的直线
的直线 的参数方程为:
的参数方程为: ,
,
直线 与曲线
与曲线 分别交于
分别交于 .
.
(Ⅰ)写出曲线 和直线
和直线 的普通方程; (Ⅱ)若
的普通方程; (Ⅱ)若 成等比数列,求
成等比数列,求 的值.
的值.
(本小题满分10分)
已知 的最大值为
的最大值为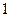 .
.
(1)求常数a的值;
(2)求使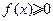 成立的x的取值范围.
成立的x的取值范围.
已知:函数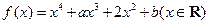 ,其中
,其中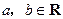 .
.
(1)当 时,讨论函数
时,讨论函数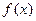 的单调性;
的单调性;
(2)若对于任意的 ,不等式
,不等式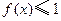 在
在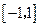 上恒成立,求
上恒成立,求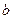 的取值范围.
的取值范围.
已知: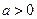 ,
,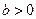 ,
,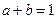 ,
,
(1)求证: ;(2)求:
;(2)求: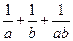 的最小值。
的最小值。
(本小题满分12分)
某工厂师徒二人各加工相同型号的零件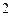 个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为
个,是否加工出精品均互不影响.已知师父加工一个零件是精品的概率为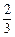 ,师徒二人各加工
,师徒二人各加工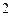 个零件都是精品的概率为
个零件都是精品的概率为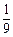 。
。
(1)求:徒弟加工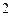 个零件都是精品的概率;
个零件都是精品的概率;
(2)求:徒弟加工该零件的精品数多于师父的概率;
(3)设师徒二人加工出的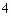 个零件中精品个数为
个零件中精品个数为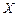 ,求:
,求: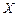 的分布列与均值
的分布列与均值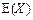 。
。
(本小题满分10分)
已知:如图,四边形ABCD内接于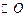 ,
,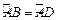 ,过
,过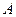 点的切线交
点的切线交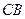 的延长线于
的延长线于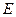 点.
点.
求证: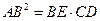 。
。