.如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=40°
(1)求证:EF⊥平面BCE;
(2)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE
(3)求二面角F—BD—A的大小。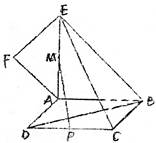
已知向量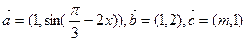
(I)若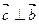 ,求实数
,求实数 的值.
的值.
(II)若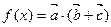 ,①求
,①求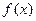 的所有对称轴方程.②求
的所有对称轴方程.②求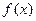 在
在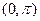 上的单调增区间.
上的单调增区间.
(本小题满分14分)
已知数列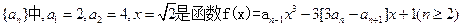 的一个极值点。
的一个极值点。
(1)证明:数列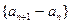 是等比数列;
是等比数列;
(II)求数列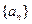 的通项公式;
的通项公式;
(III)设
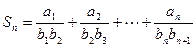 ,求证:
,求证: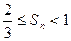
(本小题满分13分)已知点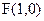 ,直线
,直线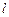 :
: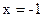 ,
,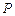 为平面上的动点,过点
为平面上的动点,过点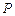 作直线
作直线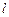 的垂线,垂足为
的垂线,垂足为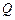 ,且
,且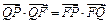 .(1)求动点
.(1)求动点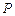 的
的 轨迹
轨迹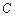 的方程;
的方程;
(2)已知点A(m,2)在曲线C上,过点A作曲线C的两条弦AD,AE,且AD,AE的斜率k1、k2满足 ,试推断:动直线DE是否过定点?证明你的结论。
,试推断:动直线DE是否过定点?证明你的结论。
(本小题满分12分)已知函数 .
.
(1)当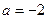 时,求函数
时,求函数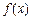 的单调区间和极值;
的单调区间和极值;
(2)当 时,试求方程
时,试求方程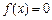 根的个数.
根的个数.
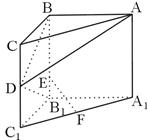
(本小题满分12分)如图,在直三棱柱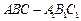 中,
中, ,
, ,
,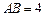 ,
,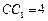 ,E在
,E在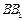 上,且
上,且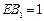 ,
,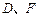 分别为
分别为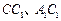 的中点.
的中点.
(1)求证: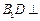 平面
平面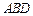 ;
;
(2)求异面直线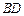 与
与 所成的角;
所成的角;
(3)求点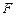 到平面
到平面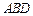 的距离.
的距离.