计算:
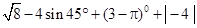
先化简,再求值:
 ,其中
,其中
如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.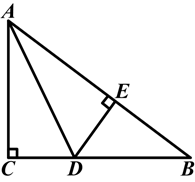
(1)求DE的长;
(2)求△ADB的面积.
如图是用硬纸板做成的四个全等的直角三角形(两直角边长分别是a、b,斜边长为c)和一个正方形(边长为c).请你将它们拼成一个能验证勾股定理的图形.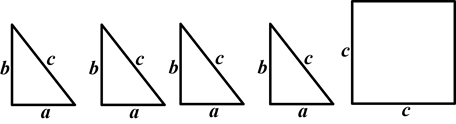
(1)画出拼成的这个图形的示意图;
(2)用(1)中画出的图形验证勾股定理.
某车间加工螺钉和螺母,当螺钉和螺母恰好配套(一个螺钉配一个螺母)时就可以包装运进库房.若一名工人平均每天可以加工螺钉120个或螺母96个,该车间共有工人81名,则应怎样分配人力,才能使每天生产出来的零件及时包装运进库房?
王阿姨和李奶奶一起去超市买菜,王阿姨买西红柿、茄子、青椒各1千克,共花了12.8元,李奶奶买西红柿2千克、茄子1.5千克,共花了15元.已知青椒每千克4.2元,请你求出每千克西红柿、茄子各多少元?
如图,Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△ADB的面积.