一次远足,小明与小聪分别从A,B两个景点出发,沿同一条公路相向而行。他们出发的时间是上午8:00,小聪行走的速度是小明的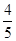 , A,B两个景点之间的路程是9千米.设小明行走的速度为x千米/小时.
, A,B两个景点之间的路程是9千米.设小明行走的速度为x千米/小时.经过t小时,在小明和小聪相遇前,他们相距多少千米?
如果小聪行走的速度是4千米/小时,那么到几时几分,小明与小聪相距3千米?
定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.
如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.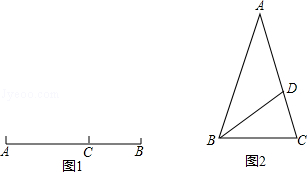
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
莆田素有“文献名邦”之称,某校就同学们对“莆田历史文化”的了解程度进行随机抽样调查,将调查结果制成如图所示的两幅统计图: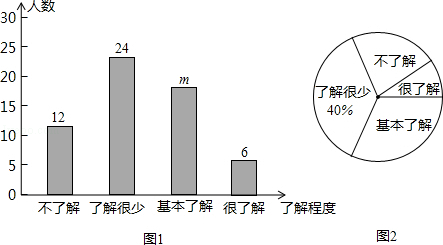
根据统计图的信息,解答下列问题:
(1)本次共调查 名学生;
(2)条形统计图中m= ;
(3)若该校共有学生1000名,则该校约有 名学生不了解“莆仙历史文化”.
先化简,再求值: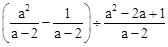 ,其中a=3.
,其中a=3.
如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2。C2的图象与x轴交于A、B两点(点A在点B的左侧)。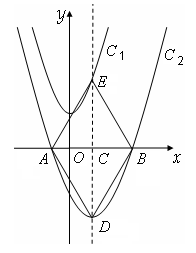
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,如果存在,请求出点G的坐标,如果不存在,请说明理由。
如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED。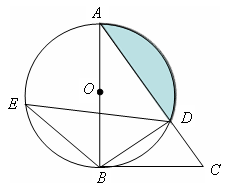
(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)若tanE=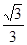 ,BC=
,BC=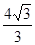 ,求阴影部分的面积。(计算结果精确到0.1)
,求阴影部分的面积。(计算结果精确到0.1)
(参考数值:π≈3.14, 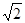 ≈1.41,
≈1.41,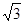 ≈1.73)
≈1.73)