某人在距离地面2.6m的高处,将质量为0.2Kg的小球以vo=12m/S速度斜向上抛出,小球的初速度方向与水平方向之间的夹角为30°,g取10m/S2,求
(1)人抛球时对球做多少功?
(2)若不计空气阻力,小球落地时的速度大小是多少?
(3)若小球落地时的速度大小为V1=13m/S,小球在空中运动过程中克服阻力做了多少功?
若你用通过同步卫星转发的无线电话与对方通话,则在你讲完话后,至少要等多长时间才能听到对方的回话(已知地球质量M=6.0×1024kg,地球半径R=6.4×106m,万有引力恒量G=6.67×10-11N·m3/kg2)?
一台收音机在中波段接收的波长范围为545.5~187.5m.
(1)求此波长范围所对应的频率范围;
(2)设该收音机接收回路由LC振荡电路组成,其中可变电容器最大电容为360pF,求线圈电感L值.
一个LC振荡电路,电感L变化的范围是0.1~4.0mH,电容C的变化范围是4~90PF,求此振荡电路的频率范围和产生的电磁波的波长范围。
在离地80 m处无初速释放一小球,小球质量为m="200" g,不计空气阻力,g取10 m/s2,取最高点所在水平面为零势能参考面.求:
(1)在第2 s末小球的重力势能
(2)在第3 s内重力所做的功,重力势能的变化.
质量为30kg的小孩坐在10kg的雪橇上,大人用与水平方向成37°斜向上的拉力拉雪橇,力的大小为100N,雪橇与地面间的动摩擦因数为0.2,求: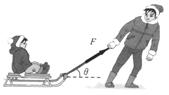
(1)雪橇对地面的压力大小(sin37°=0.6,cos37°=0.8 ,g=10m/s2)
(2)雪橇运动的加速度大小
(3)若沿相反的方向施加大小相同的推力,则从静止开始1分种后,雪橇的速度多大?通过的位移是多少?