已知函数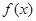 满足
满足 =
= ,(其中a>0且a≠1)
,(其中a>0且a≠1)
(1)求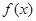 的解析式及其定义域;
的解析式及其定义域;
(2)在函数 的图像上是否存在两个不同的点,使过两点的直线与x轴平行,如果存在,求出两点;如果不存在,说明理由。
的图像上是否存在两个不同的点,使过两点的直线与x轴平行,如果存在,求出两点;如果不存在,说明理由。
设各项均为正数的数列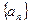 的前n项和为
的前n项和为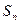 ,已知
,已知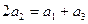 ,数
,数
列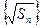 是公差为
是公差为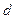 的等差数列。
的等差数列。
(1)求数列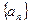 的通项公式(用
的通项公式(用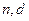 表示);
表示);
(2)设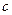 为实数,对满足
为实数,对满足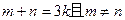 的任意正整数
的任意正整数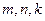 ,不等式
,不等式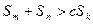 都成立。求证:
都成立。求证: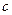 的最大值为
的最大值为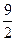 。
。
设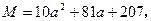
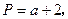
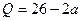 ,若将
,若将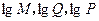
适当排序后可构成公差为1的等差数列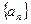 的前三项.
的前三项.
(Ⅰ)求
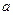 的值及
的值及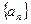 的通项公式;
的通项公式;
(Ⅱ )记函数
)记函数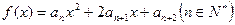 的图象在
的图象在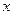 轴上截得的线段长为
轴上截得的线段长为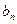 ,设
,设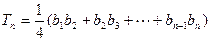 ,求
,求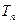
 证明以下命题:
证明以下命题:
(Ⅰ)对任一正整a,都存在整数b,c(b<c),使得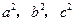 成等差数列。
成等差数列。
(Ⅱ)存在无穷多个互不相似的三角形△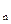 ,其边长
,其边长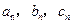 为正整数且
为正整数且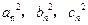 成等差数列。
成等差数列。
在数列 中,
中, =0,且对任意k
=0,且对任意k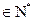 ,
, 成等差数列,
成等差数列,
其公差为2k。
(Ⅰ)证明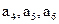 成等比数列;
成等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
已知 为等差数列,且
为等差数列,且 ,
,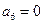 。
。
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)若等差数列 满足
满足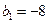 ,
, ,求
,求 的前n项和公式
的前n项和公式