电焊工想利用一块边长为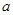 的正方形钢板
的正方形钢板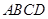 做成一个扇形,于是设计了以下三种方案:
做成一个扇形,于是设计了以下三种方案:
方案一:如图1,直接从钢板上割下扇形 .
.
方案二:如图2,先在钢板上沿对角线割下两个扇形,再焊接成一个大扇形(如图3).
方案三:如图4,先把钢板分成两个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将四个小扇形按与图3类似的方法焊接成一个大扇形.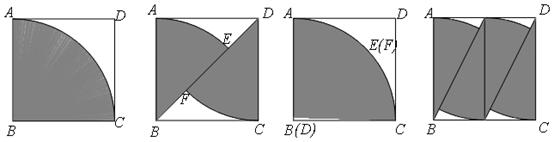
图1 图2 图3容易得出图1、图3中所得扇形的圆心角均为
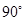 ,那么按方案三所焊接成的大扇形的圆心角也为
,那么按方案三所焊接成的大扇形的圆心角也为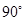 吗?为什么?
吗?为什么?容易得出图1中扇形与图3中所得大扇形的面积相等,那么按方案三所焊成的大扇形的面积也与方案二所焊接成的大扇形的面积相等吗?若不相等,面积是增大还是减小?为什么?
若将正方形钢板按类似图4的方式割成
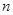 个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这
个相同的小矩形,并在每个小矩形里割下两个小扇形,然后将这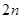 个小扇形按类似方案三的方式焊接成一个大扇形,则当
个小扇形按类似方案三的方式焊接成一个大扇形,则当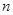 逐渐增大时,所焊接成的大扇形的面积如何变化?
逐渐增大时,所焊接成的大扇形的面积如何变化?
两幢垂直于地面的大楼相距110米,从甲楼顶部看乙楼顶部的仰角为30°,已知甲楼高35米根据题意,在图中画出示意图;
求乙楼的高度为多少米?
“戒烟一小时,健康亿人行”.今年国际无烟日,小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:A.顾客出面制止;B.劝说进吸烟室;C.餐厅老板出面制止;D.无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题: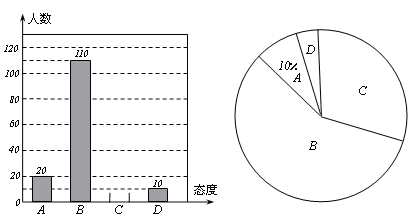
求这次抽样的公众有多少人?
请将统计图①补充完整
在统计图②中,求“无所谓”部分所对应的圆心角是多少度?
若城区人口有20万人,估计赞成“餐厅老板出面制止”的有多少万人?
小华在城区中心地带随机对路人进行调查,请你根据以上信息,求赞成“餐厅老板出面制止”的概率是多少?
计算
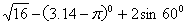 .
.画出函数y=-x2+1的图象
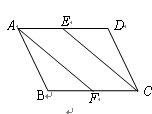
已知:如图,E,F分别是□ABCD的边AD,BC的中点.求证:AF=CE.
如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AB=6,RtA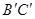 可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段
可以看作是由Rt△ABC绕点A逆时针方向旋转60°得到的,则线段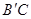 的长为_________________.
的长为_________________.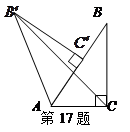
如图①,二次函数的抛物线的顶点坐标C,与x轴的交于A(1,0)、B(-3,0)两点,与y轴交于点D(0,3)求这个抛物线的解析式
如图②,过点A的直线与抛物线交于点E,交
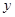 轴于点F,其中点E的横坐标为-2,若直线
轴于点F,其中点E的横坐标为-2,若直线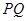 为抛物线的对称轴,点G为直线
为抛物线的对称轴,点G为直线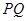 上的一动点,则
上的一动点,则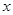 轴上是否存在一点H,使
轴上是否存在一点H,使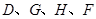 四点所围成的四边形周长最小,若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
四点所围成的四边形周长最小,若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;如图③,连接AC交y轴于M,在x轴上是否存在点P,使以P、C、M为顶点的三角形与△AOM相似?若存在,求出点P的坐标;若不存在,请说明理由.
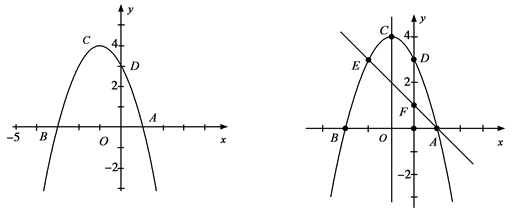
图①图②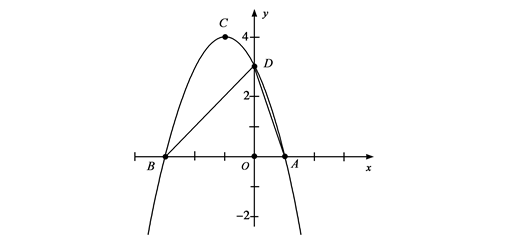
图③