如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,
求证:平面A B1D1∥平面EFG;
(2) 求证:平面AA1C⊥面EFG.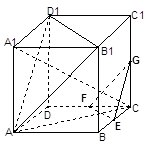
田忌和齐王赛马是历史上有名的故事,设齐王的三匹马分别为A、B、C,田忌的三匹马分别为a、b、c;三匹马各比赛一次,胜两场者为获胜。若这六匹马比赛优、劣程度可以用以下不等式表示: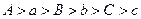
(1)正常情况下,求田忌获胜的概率
(2)为了得到更大的获胜机会,田忌预先派出探子到齐王处打探实情,得知齐王第一场必出上等马A,于是田忌采用了最恰当的应对策略,求这时田忌获胜的概率
已知关于 的方程
的方程 的两根为
的两根为 和
和 ,
,
(1)求 的值 (2)求
的值 (2)求 的值 (3)求
的值 (3)求 的值
的值
为了了解学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,所得数据整理后,画出频率分布直方图(如右),图中从左到右各小长方形面积之比为 ,第二小组频数为12
,第二小组频数为12
(1) 学生跳绳次数的中位数落在哪个小组内?
(2) 第二小组的频率是多少?样本容量是多少? (3) 若次数在110以上(含110次)为良好,试估计该学校全体高一学生的良好率是多少?
(3) 若次数在110以上(含110次)为良好,试估计该学校全体高一学生的良好率是多少?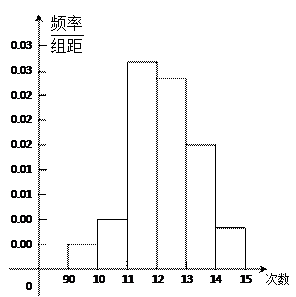
已知: ,求
,求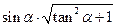 的值
的值
求值: