航模兴趣小组设计出一架遥控飞行器,其质量m =2㎏,动力系统提供的恒定升力F ="28" N。试飞时,飞行器从地面由静止开始 竖直上升。设飞行器飞行时所受的阻力大小不变,g取10m/s2。
竖直上升。设飞行器飞行时所受的阻力大小不变,g取10m/s2。第一次试飞,飞行器飞行t1 =" 8" s 时到达高度H =" 64" m。求飞行器所阻力f的大小;
第二次试飞,飞行器飞行t2 =" 6" s 时遥控器出现故障,飞行器立即失去升力。求飞行器
 能达到的最大高度h;
能达到的最大高度h;为了使飞行器不致坠落到地面,求飞行器从开始下落到恢复升力的最长时间t3。
[物理—选修3—5]
(1)下列说法正确的是。
| A.光电效应现象显示了光的粒子性,它否定了光的波动性 |
| B.为了解释原子光谱的不连续性,普朗克提出能量量子化观点 |
| C.某元素原子核内的质子数决定了核外电子的分布,进而决定了该元素的化学性质 |
| D.核力是短程力,在其作用范围内,随核子间距离的变化可以表现为引力也可以表现为斥力 |
(2)贫铀合金具有高密度、高强度、高韧性的特点,用它做弹芯穿甲能力强,可以摧毁坚固的目标。贫铀弹的重要原料是铀238,具有放射性,放出的射线对人体会造成严重的伤害,因此爱好和平的人们都反对使用贫铀弹。若某静止的铀核(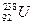 )发生
)发生 衰变生成钍核(Th),并同时放出能量为E的
衰变生成钍核(Th),并同时放出能量为E的 光子,已知铀核的质量为
光子,已知铀核的质量为 ,钍核的质量为
,钍核的质量为 粒子的质量为
粒子的质量为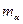 。
。
①写出核反应方程。
②若放出的 光子动量可忽略,求衰变生成的
光子动量可忽略,求衰变生成的 粒子的速率。
粒子的速率。
[物理—选修3—5]
(1)下列说法正确的是。
| A.在光导纤维束内传送图像是利用光的全反射现象 |
| B.拍摄玻璃橱窗内的物品时,往往在镜头前加装一个偏振片以增加透射光的强度 |
| C.在受迫振动中驱动力的频率总是等于物体的固有频率 |
| D.可见光只是电磁波中的一小部分,可见光的频率低于X射线的频率 |
(2)有一玻璃球冠,右侧面镀银,光源S就在其对称轴上,如图21所示。从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折入玻璃球冠内,经右侧镀银面第一次反射恰能沿原路返回。若球面半径为R,玻璃折射率为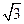 ,求光源S与球冠顶点M之间的距离SM为多大?
,求光源S与球冠顶点M之间的距离SM为多大?
[物理——选修3-3]
(1)( 5分)下列说法中正确的是。
5分)下列说法中正确的是。
| A.布朗运动是液体分子的运动,它说明分子永不停息地做无规则运动 |
| B.叶面上的小露珠呈球形是由于液体表面张力的作用 |
| C.液晶显示器是利用了液晶对光具有各向异性的特点 |
| D.当两分子间距离大于平衡位置的间距r0时,分子间的距离越大,分子势能越小 |
(2)如图20所示,开口向上竖直放置的内壁光滑气缸,其侧壁是绝热的,底部导热,内有两个质量均为m的密闭活塞,活塞A导热,活塞B绝热,将缸内理想气体分成I、II两部分。初状态整个装置静止不动处于平衡,I、II两部分气体的长度均为l0,温度为T0。设外界大气压强为P0保持不变,活塞横截面积为S,且mg=P0S,环境温度保持不变。求:
①在活塞A上逐渐添加铁砂,当铁砂质量等于2m时,两活塞在某位置重新处于平衡,活塞B下降的高度。
②现只对II气体缓慢加热,使活塞A回到初始位置,此时II气体的温度。
许多仪器中可利用磁场控制带电粒子的运动轨迹。如图11所示的真空环境中,有一半径r=0.05m的圆形区域内存在磁感应强度B=0.2T的匀强磁场,其右侧相距d=0.06m处有一足够大的竖直屏。从S处不断有比荷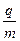 =108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上。不计粒子重力,求:
=108C/kg的带正电粒子以速度v=2×106m/s沿SQ方向射出,经过磁场区域后打在屏上。不计粒子重力,求:
(1)粒子在磁场中做圆周运动的轨迹半径;
(2)绕通过P点垂直纸面的轴,将该圆形磁场区域逆时针缓慢转动90°的过程中,粒子在屏上能打到的范围。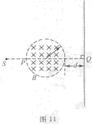
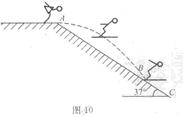
2010年冬奥会上跳台滑雪是一项极为壮观的运动,将其运动过程简化为如图10所示,运动员穿着滑雪板,从跳台水平飞出,在空中飞行一段距离后着陆。若运动员和滑雪板等装备的总质量为70kg,从倾角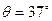 的坡顶A点以速度v0=20m/s沿水平方向飞出,能落到雪坡上的B处。运动员落到雪坡上不弹起,磁撞中动能损失了20%,在雪坡上滑动过程中所受阻力为运动员和滑雪板等装备总重力的0.3倍,又下滑10m到C点,忽略空气阻力影响。(g=10m/s2,sin37°=0.6)求:
的坡顶A点以速度v0=20m/s沿水平方向飞出,能落到雪坡上的B处。运动员落到雪坡上不弹起,磁撞中动能损失了20%,在雪坡上滑动过程中所受阻力为运动员和滑雪板等装备总重力的0.3倍,又下滑10m到C点,忽略空气阻力影响。(g=10m/s2,sin37°=0.6)求:
(1)运动员在空中飞行的时间t和AB间的距离s;
(2)下滑到C点时的动能Ek.