如下图,在xOy坐标系的第一象限内有互相正交的匀强电场E与匀强磁场B,E的大小为1.0×103V/m,方向未知,B的大小为1.0T,方向垂直纸面向里;第二象限的某个圆形区域内,有方向垂直纸面向里的匀强磁场B′。一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与x轴负方向60°角从A点沿直线进入第一象限运动,经B点即进入处于第二象限内的磁场B′区域,一段时间后,微粒经过x轴上的C点并与x轴负方向成60°角的方向飞出。已知A点的坐标为(10,0),C点的坐标为(-30,0),不计粒子重力,g取10m/s2。请分析判断匀强电场E的方向并求出微粒的运动速度v;
匀强磁场B′的大小为多大?
B′磁场区域的最小面积为多少?

(14分)一小石块从空中自由下落h=5m后,掉入淤泥,落到淤泥底时速度恰好为零,全过程共用时t=1.2s。假设石块在淤泥中做匀减速直线运动,且g=10m/s2,则:
(1)小石块掉入淤泥前的瞬时速度 大小为多少;
大小为多少;
(2)石块陷入淤泥的深度d及此过程石块的加速度 的大小
的大小
一质点沿直线运动,其速度随时间变化的情况如图所示,设向右为正方向。由图求:
(1)质点在AB、BC分别做什么运动?
(2)质点在OA段的加速度
(3)质点在8s内的位移
(10分)如图所示,倾角为θ的斜面AB是粗糙且绝缘的,AB长为L,C为AB的中点,在A、C之间加一方向垂直斜面向上的匀强电场,与斜面垂直的虚线CD为电场的边界。现有一质量为m、电荷量为q的带正电的小物块(可视为质点),从B点开始在B、C间以速度υ0沿斜面向下做匀速运动,经过C后
沿斜面匀加速下滑,到达斜面底端A时的速度大小为υ。试求:
(1)小物块与斜面间的动摩擦因数μ;
(2)匀强电场场强E的大小。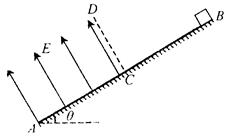
有一电荷量q=—2×10-6 C的点电荷从电场中的A点移到B点时,克服电场力做功6×10-4 J,从B点移到C点时电场力做功9×10-4 J,问
(1)AB、BC间的电势差各为多少?
(2)若取A点电势为零,则C点的电势为多少?
.质量为500吨的机车以恒定的功率由静止出发,经5min行驶2.25km,速度达到最大值54km/h,设阻力恒定。问:
(1)机车的功率P多大?
(2)机车的速度为36 km/h时机车的加速度a多大?