如下图（a）所示，间距为l、电阻不计的光滑导轨固定在倾角为θ的斜面上。在区域I内有方向垂直于斜面的匀强磁场，磁感应强度为B；在区域Ⅱ内有垂直于斜面向下的匀强磁场，其磁感应强度Bt的大小随时间t变化的规律如下图（b）所示。t=0时刻在轨道上端的金属细棒ab从如图位置由静止开始沿导轨下滑，同时下端的另一金属细棒cd在位于区域I内的导轨上由静止释放。在ab棒运动到区域Ⅱ的下边界EF处之前，cd棒始终静止不动，两棒均与导轨接触良好。已知cd棒的质量为m、电阻为R，ab棒的质量、阻值均未知，区域Ⅱ沿斜面的长度为2l，在t=tx时刻（tx未知）ab棒恰进入区域Ⅱ，重力加速度为g。求：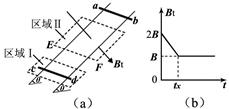
通过cd棒电流的方向和区域I内磁场的方向；
当ab棒在区域Ⅱ内运动时cd棒消耗的电功率；
ab棒开始下滑的位置离EF的距离；
ab棒开始下滑至EF的过程中回路中产生的热量。
物体从静止开始做匀加速直线运动，前2s内的位移是8m，试求以下问题。
①第3s内位移。
②速度从6m / s增至10m / s发生的位移。
如图所示，两块水平放置、相距为
的长金属板接在电压可调的电源上。两板之间的右侧长度为
的区域存在方向垂直纸面向里的匀强磁场，磁感应强度为
。喷墨打印机的喷口可在两极板左侧上下自由移动，并且从喷口连续不断喷出质量均为
、速度水平且大小相等、带等量电荷的墨滴。调节电源电压至
，使墨滴在电场的左侧区域恰能沿水平方向向右做匀速直线运动。（重力加速度为
）
（1）判断墨滴所带电荷的种类，并求其电荷量；
（2）要使墨滴不从两板间射出，求墨滴的入射速率应满足的条件。
一小型发电站通过升压、降压变压器把电能输给用户。已知发电机的输出功率是
，端电压为
，升压变压器原、副线圈的匝数比为1:8，两变压器间输电线的总电阻为
，降压变压器的输出电压为
，不计变压器的损耗。求：
（1）升压变压器的副线圈两端电压；
（2）输电导线上的功率损失；
（3）降压变压器原、副线圈的匝数比；
（4）用户得到的功率。
如图所示，水平面上有两根相距
的足够长的光滑平行金属导轨
和
，它们的电阻可忽略不计，在
和
之间接有阻值为
的定值电阻。导体棒
长
，其电阻为
，与导轨接触良好。整个装置处于方向竖直向上的匀强磁场中，磁感应强度
。现在在导体棒ab上施加一个水平向右的力
，使以
的速度向右做匀速运动时，求：
⑴中的感应电动势多大？
⑵中电流的方向如何？
⑶若定值电阻
，导体棒的电阻
，则多大？
某理想变压器的原、副线圈匝数比n1：n2=55:9，原线圈上的正弦交变电压U1=220V，试求：（1）副线圈上的输出电压为多大？
（2）若副线圈输出的功率为10W变压器的输入功率为多少？