计算(每小题4分,共8分):(1)
 .
.(2)
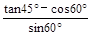 ·tan 30°.
·tan 30°.
已知关于 的一元二次方程 有实数根.
(1)求 的取值范围;
(2)若此方程的两实数根 , 满足 ,求 的值.
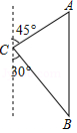
如图,一艘海轮位于灯塔 的北偏东 方向,距离灯塔100海里的 处,它沿正南方向航行一段时间后,到达位于灯塔 的南偏东 方向上的 处,求此时船距灯塔的距离(参考数据: , ,结果取整数).
化简:
计算:
阅读理解:在平面直角坐标系中,若两点 、 的坐标分别是 , 、
, ,则 、 这两点间的距离为 .如 , ,则 .
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
解决问题:如图,已知在平面直角坐标系 中,直线 交 轴于点 ,点 关于 轴的对称点为点 ,过点 作直线 平行于 轴.
(1)到点 的距离等于线段 长度的点的轨迹是 ;
(2)若动点 满足到直线 的距离等于线段 的长度,求动点 轨迹的函数表达式;
问题拓展:(3)若(2)中的动点 的轨迹与直线 交于 、 两点,分别过 、 作直线 的垂线,垂足分别是 、 ,求证:
① 是 外接圆的切线;
② 为定值.
