已知直角梯形纸片OABC在平面直角坐标系中的位置如图①所示，四
个顶点的坐标分别为O(0，0)，A(10，0)，B(8，2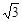
)，C(0，2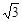)，点P在线段OA上(不与O、A重合)，将纸片折叠，使点A落在射线AB上(记为点A’)，折痕PQ与射线AB交于点Q，设OP＝x，折叠后纸片重叠部分的面积为y．(图②供探索用)求∠OAB的度数；
求y与x的函数关系式，并写出对应的x的取值范围；
y存在最大值吗？若存在，求出这个最大值，并求此时x的值；若不存在，说明理由．
如图，在□ABCD中，E、F分别是边AB、CD的中点，BD是对角线，过A点作AG∥DB交CB的延长线于点G．
（1）求证：DE∥BF．
（2）若∠G＝90°，求证：四边形DEBF是菱形．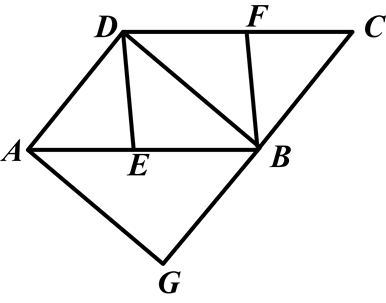
如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．
（1）求证：AF＝DC．
（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．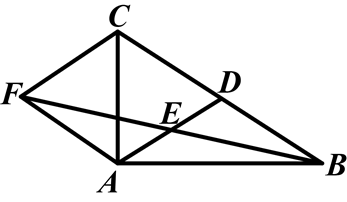
如图，在四边形ABCD中，AB＝AD，CB＝CD，E是CD上一点，BE交AC于F．连接DF．
（1）证明：∠BAC＝∠DAC，∠AFD＝∠CFE．
（2）若AB∥CD，证明：四边形ABCD是菱形．
（3）在（2）的条件下，试确定E点的位置，使∠EFD＝∠BCD，并说明理由．
如图，在△ABC中，AB＝AC，∠B＝60°，∠FAC、∠ECA是△ABC的两个外角，AD平分∠FAC，CD平分∠ECA．
求证：四边形ABCD是菱形．
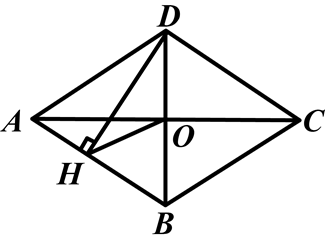
如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，求证：∠DHO＝∠DCO．