如图所示，第四象限内有互相正交的匀强电场E与匀强磁场B1， E的大小为0.5×103V/m, B1大小为0.5T；第一象限的某个矩形区域内，有方向垂直纸面向里的匀强磁场B2，磁场的下边界与x轴重合．一质量m=1×10-14kg、电荷量q=1×10-10C的带正电微粒以某一速度v沿与y轴正方向60°角从M点沿直线运动，经P点即进入处于第一象限内的磁场B2区域．一段时间后，小球经过y轴上的N点并与y轴正方向成60°角的方向飞出。M点的坐标为(0，-10)，N点的坐标为(0，30)，不计粒子重力，g取10m/s2．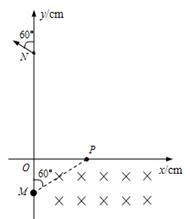
请分析判断匀强电场E的方向(要求在图中画出)并求出微粒的运动速度v；
匀强磁场B2的大小为多大？
B2磁场区域的最小面积为多少？
质量为m=2kg的物体置于水平粗糙地面上，用F=20N的水平拉力使它从静止开始运动，第4s末物体的速度达到24m/s，此时撤去拉力F。求：
(1)物体在运动中受到的阻力f；
(2)撤去拉力后物体能继续滑行的距离s
如图7所示，重量G=100N的物体置于水平面上，给物体施加一个与水平方向成θ=37°的拉力F，F=20N，物体仍处于静止状态，已知sin37°=0.6，cos37°=0.8。求：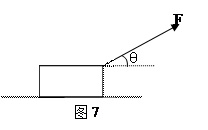
（1）地面对物体的静摩擦力；
（2）地面对物体的支持力；
（3）若μ=
，则力F要达到多大才能使物体沿水平面作匀速直线运动？
如图，光滑的平行金属导
轨水平放置，电阻不计，导轨间距为l，左侧接一阻值为R的电阻。区域cdef内存在垂直轨道平面向下的有界匀强磁场，磁场宽度为s 。一质量为m ，电阻为r的金属棒MN置于导轨上，与导轨垂直且接触良好，受到F＝0.5v＋0.4（N）（v为金属棒运动速度）的水平力作用，从磁场的左边界由静止开始运动，测得电阻两端电压随时间均匀增大。 （已知l＝1m，m＝1kg，R＝0.3W，r＝0.2W，s＝1m）
（1）该金属棒在磁场中做匀速运动还是匀加速运动？
（2）求磁感应强度B的大小；
（3）若撤去外力后棒的速度v随位移x的变化规律满足v＝v0－x，且棒在运动到ef处时恰好静止，则外力F作用的时间为多少？
如图所示,线圈内有理想边界的磁场,开始时磁场的磁感应强度为B0 . 当磁场均匀增加时,有一带电微粒静止于平行板(两板水平放置)电容器中间,若线圈的匝数为1 ,平行板电容器的板间距离为d ,粒子的质量为m,带电荷量为q.(设线圈的面积为S)求:
(1) 开始时穿过线圈平面的
磁通量的大小.
(2) 处于平行板电容器间的粒子的带电性质.
(3) 磁感应强度的变化率.
一座小型水电站，它输出的功率是20KW，输电电压是400V。输电线的总电阻是0.5W，用户得到的电功率是多少KW？