我们已经学过用方差来描述一组数据的离散程度,其实我们还可以用“平均差”来描述一组数据的离散程度。在一组数据x1,x2,…,xn中,各数据与它们的平均数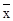 的差的绝对值的平均数,即T=
的差的绝对值的平均数,即T= (|x1-
(|x1-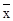 |+|x2-
|+|x2-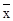 |+…+|xn-
|+…+|xn-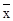 |)叫做这组数据的“平均差”,“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大。
|)叫做这组数据的“平均差”,“平均差”也能描述一组数据的离散程度,“平均差”越大说明数据的离散程度越大。
请你解决下列问题:分别计算下列甲乙两个样本数据的“平均差”,并根据计算结果判断哪个样本波动较大。
甲:12,13,11,10,14, 乙:10,17,10,13,10分别计算甲、乙两个样本数据的方差和标准差,并根据计算结果判断哪个样本波动较大.
以上的两种方法判断的结果是否一致?
二次函数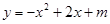 的图象与
的图象与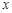 轴的一个交点为A
轴的一个交点为A ,另一个交点为B,与
,另一个交点为B,与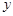 轴交于点C.
轴交于点C.
(1)求 的值及点B、点C的坐标;
的值及点B、点C的坐标;
(2)直接写出当 时,
时,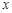 的取值范围;
的取值范围;
(3)直接写出当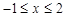 时,
时, 的取值范围.
的取值范围.
如图,甲、乙用4张扑克牌玩游戏,他俩将扑克牌洗匀后背面朝上,放置在桌面上,每人抽一张,甲先抽,乙后抽,抽出的牌不放回.甲、乙约定:只有甲抽到的牌面数字比乙大时甲胜;否则乙胜. 请你用树状图或列表法说明甲、乙获胜的机会是否相同.
如图,△ABC的顶点在格点上,且点A(-5,-1),点C(-1,-2).
(1)以原点O为旋转中心,将△ABC绕点O逆时针旋转90°得到△ . 请在图中画出△
. 请在图中画出△ ,并写出点A的对称点
,并写出点A的对称点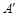 的坐标;
的坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的图形△ .
.
已知二次函数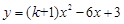 的图象与x轴有交点,求k的取值范围.
的图象与x轴有交点,求k的取值范围.
如图,小聪用一块有一个锐角为 的直角三角板测量树高,已知小聪和树都与地面垂直,且相距
的直角三角板测量树高,已知小聪和树都与地面垂直,且相距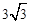 米,小聪身高AB为1.7米,求这棵树的高度.
米,小聪身高AB为1.7米,求这棵树的高度.