如图,已知AB是⊙O的直径,点D、E在⊙O上,且︵AD∶︵DE=3∶5, ︵BE的度数为20°,连接DE并延长交AB的延长线于C,求∠AOD的度数;
判断CE与AB有什么数量关系,并说明理由

为落实校园“阳光体育”工程,某校计划购买篮球和排球共20个.已知篮球每个80元,排球每个60元.设购买篮球x个,购买篮球和排球的总费用y元.
(1)求y与x之间的函数关系式;
(2)如果要求篮球的个数不少于排球个数的3倍,应如何购买,才能使总费用最少?最少费用是多少元?
已知一次函数的图象经过点(3,5)与(-4,-9).
(1)求这个函数的解析式;
(2)判断点A(1,-1)和点B(2.5,4)是否在这个函数的图象上.
△ABC在平面直角坐标系中的位置如右图所示.
(1)直接写出点A的坐标;
(2)作出△ABC关于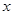 轴对称的△
轴对称的△ ,并分别写出点
,并分别写出点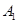 ,B1,C1的坐标
,B1,C1的坐标
(1)解方程: ;(2)
;(2)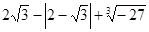
老王带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一 些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)老王自带的零钱是多少?
(2)试求降价前y与x之间的关系式.
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?