(本题8分)水坝的横断面为梯形ABCD,迎水坡BC的坡角B为30°,背水坡AD坡比为1:1.5,坝顶宽DC=2米,坝高4米,求: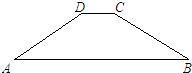
(1)坝底AB的长;
(2)迎水坡BC的坡比.
为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
如图,点C是以AB为直径的⊙O上的一点,AD与过点C的切线互相垂直,垂足为点D.
(1)求证:AC平分∠BAD;
(2)若CD=1,AC= ,求⊙O的半径长.
,求⊙O的半径长.
如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为45°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度为 (即tan∠PCD=
(即tan∠PCD= ).
).
(1)求该建筑物的高度(即AB的长).
(2)求此人所在位置点P的铅直高度.(测倾器的高度忽略不计,结果保留根号形式)
小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
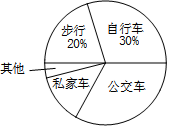
某中学为了解全校学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).请根据图中提供的信息解答下列问题: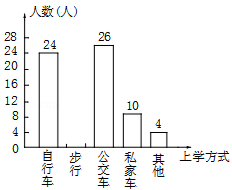
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)在扇形统计图中,“公交车”部分所对应的圆心角是多少度?
(4)若全校有1600名学生,估计该校乘坐私家车上学的学生约有多少名?