你还记得图形的旋转吗？如图，P是正方形ABCD内一点，PA=a，PB=2a，PC=3a.将△APB绕点B按顺时针方向旋转，使AB与BC重合，得△CBP，求证：△PBP，是等腰直角三角形;
猜想△PCP，的形状，并说明理由.（考查逻辑推理能力）
有两个水池，甲水池装满水，长8米，宽6米，水深3米，乙水池空着，它长、宽、高都是4米．现将从甲水池中抽出一部分水到乙水池，使两水池的水面同样高．求水面的高度．
学校举行“六一”庆祝活动，六（1）班有30人参加演出，比六（2）班参加演出的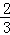
多6人，六（2）班有多少人参加了节目演出？（用方程解）
在比例尺为1：30000的地图上，量得一条公路长5厘米，由甲、乙两队合修需要6天完成．甲乙两队的工作效率比是2：3，求甲队每天修路多少米？
小丽看一本书，第一天看了28页，第二天看了22页，她两天一共看了全书的
，这本书有多少页？
客车、货车两车同时从甲、乙两城相对开出，客车每小时行60千米，是货车速度的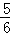
，两车开出后6小时相遇．甲、乙两城相距多少千米？