(本小题满分13分)
已知椭圆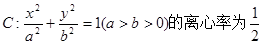 ,以原点为圆心,椭
,以原点为圆心,椭 圆的短半轴为半径的圆与直线
圆的短半轴为半径的圆与直线 相切.
相切.
(1)求椭圆C的方程;
(2)设 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结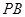 交椭圆
交椭圆
于另一点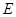 ,证明:直线
,证明:直线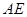 与x轴相交于定点
与x轴相交于定点
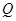 ;
;
(3) 在(2)的条件下,过点
在(2)的条件下,过点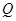 的直线与椭圆
的直线与椭圆 交于
交于 、
、 两点,求
两点,求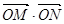 的取值
的取值
范围.
(本小题满分12分)
下列三个图中,左边是一个正方体截去一个角后所得多面体的直观图。右边两个是正视图和侧视图.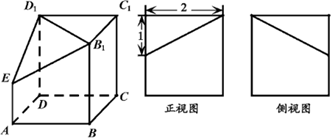
(1)请在正视图的下方,按照画三视图的要求画出该多面体的俯视图(不要求叙述作图过程);
(2)求该多面体的体积(尺寸如图).
(本小题满分12分)
已知直线l1经过A(1,1)和B(3,2),直线l2方程为2x-4y-3=0.
(1)求直线l1的方程;
(2)判断直线l1与l2的位置关系,并说明理由。
(本小题满分10分) 已知角 的终边经过点
的终边经过点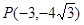 求
求 的值。
的值。
(本小题满分12分)已知
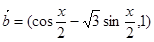
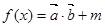
(1) 求 在
在 上的单调区间
上的单调区间
(2)当x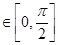 时,
时, 的最小值为2,求
的最小值为2,求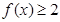 成立的
成立的 的取值集合。
的取值集合。
(3)若存在实数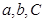 ,使得
,使得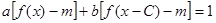 ,对任意x
,对任意x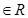 恒成立,
恒成立,
求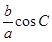 的值。
的值。
(本小题满分12分)在 中,
中, 为
为 的中点,
的中点,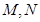 分别在
分别在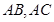 上,且
上,且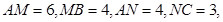
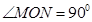 ,求
,求 的值。
的值。