2010年4月14日清晨7时49分，青海玉树发生了7.1级强烈地震，伤亡巨大，损伤惨重．某市某中学某班为灾区献爱心的捐款活动进行了抽样调查，结果如图所示．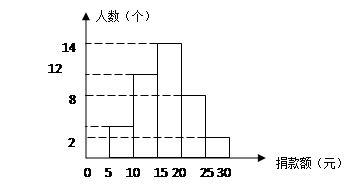
若捐款在10～15元的频率为0.3，则捐款额在10元以下的学生有多少人？
若从中任意抽取一位同学，则该同学的捐款额在15元以上的概率是多少？
若该校共有学生1600人，估计全校学生一共捐款多少元？
已知：a、b互为相反数，c、d互为倒数，x的绝对值为2，求：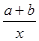
＋x3–cd的值：
先化简，再求值：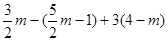
，其中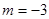
。
化简：
（1）
；
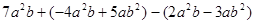（2）5x2－[x2＋（5x2－2x）－ 2（x2－3x）] .
（1）
；
（2）
.
如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A（1，2），过A、C两点的直线分别交x轴、y轴于点E、F．抛物线y=ax2+bx+c经过O、A、C三点．
（1）求该抛物线的函数解析式；
（2）点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由．
（3）若△AOB沿AC方向平移（点A始终在线段AC上，且不与点C重合），△AOB在平移过程中与△COD重叠部分面积记为S．试探究S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．