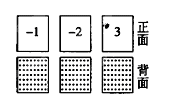
有3张不透明的卡片,除正面写有不同的数字外,其他均相同.将这三张卡片背面朝上洗匀后,第一次从中随机抽取一张,并把这张卡片标有的数字记作一次函数表达式中的k,第二次从余下的两张卡片中再随机抽取一张,上面标有的数字记作一次函数表达式中的b写出k为负数的概率

先化简,再求值: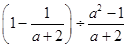 ,其中,
,其中,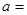 3.
3.
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE.设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C、F、D的抛物线为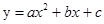 .
.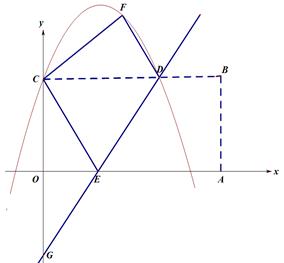
(1)求点D的坐标(用含m的式子表示)
(2)若点G的坐标为(0,-3),求该抛物线的解析式.
(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使PM=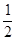 EA?若存在,直接写出P的坐标,若不存在,说明理由.
EA?若存在,直接写出P的坐标,若不存在,说明理由.
如图,在
中,点
、
、
分别在
、
、
上,且
,
.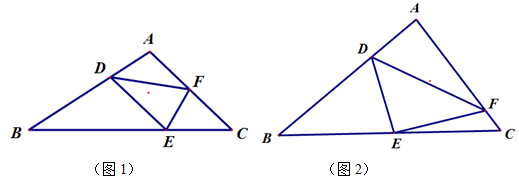
(1)如图1,当
时,图1中是否存在于
相等的线段?若存在,请找出并加以证明.若不存在说明理由.
(2)如图2,当
(其中
)时,若
,
,求
的长(用含
,
的式子表示).
如图1,在△ABC中,∠C=90°,点D在AC上,且CD>DA,DA=2.点P、Q同时从D点出发,以相同的速度分别沿射线DC、射线DA运动.过点Q作AC的垂线段QR,使QR=PQ,联接PR.当点Q到达A时,点P、Q同时停止运动.设PQ=x.△PQR和△ABC重合部分的面积为S.S关于x的函数图像如图2所示(其中0<x≤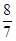 ,
,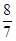 <x≤m时,函数的解析式不同)
<x≤m时,函数的解析式不同)
(1)填空:n的值为___________;
(2)求S关于x的函数关系式,并写出x的取值范围.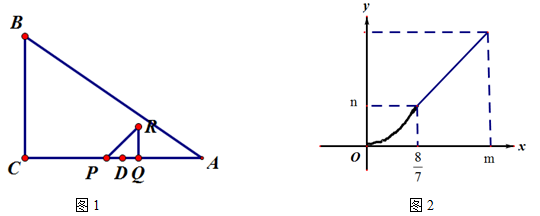
如图,AB是圆O的直径,点C、D在圆O上,且AD平分∠CAB.过点D作AC的垂线,与AC的延长线相交于E,与AB的延长线相交于点F.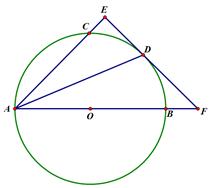
(1)求证:EF与圆O相切;
(2)若AB=6,AD=4 ,求EF的长.
,求EF的长.