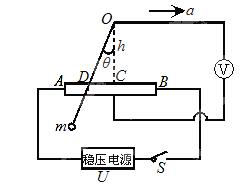
如图所示是一种悬球式加速度仪，它可以用来测定沿水平轨道做匀加速直线运动的列车的加速度。m是一个金属球，它系在细金属丝的下端，金属丝的上端悬挂在O点，AB是一根长为l的电阻丝，其阻值为R。金属丝与电阻丝接触良好，摩擦不计。电阻丝的中点C焊接一根导线.从O点也引出一根导线，两线之间接入一个电压表V（金属丝和导线电阻不计）。图中虚线OC与AB相垂直，且OC=h，电阻丝AB接在电压恒为U的直流稳压电源上。整个装置固定在列车中使AB沿着车前进的方向。列车静止时金属丝呈竖直状态；当列车加速或减速前进时，金属线将偏离竖直方向θ，从电压表的读数变化可以测出加速度的大小。当列车向右做匀加速直线运动时，试写出加速度a与θ角的关系及加速度a与电压表读数U′的对应关系。
这个装置能测得的最大加速度是多少?
如图所示，离子源从小孔发射出带电量为e的正离子（初速可忽略），在加速电压U的作用下，沿MO方向进入匀强磁场中，磁场限制在以O为圆心，半径为r的区域内，磁感应强度为B，方向垂直纸面向外，离子从N点射出，已知
（不计重力），则正离子质量为多少？正离子通过磁场所需的时间为多少？
如图所示，匀强磁场沿水平方向，垂直纸面向里，磁感强度B=1T，匀强电场方向水平向右，场强
N/C。一带正电的微粒质量m=2×10-6kg，电荷量q=2×10-6C，在此空间恰好做匀速直线运动，问：
（1）带电微粒运动速度的大小和方向怎样？
（2）若微粒运动到P点时刻，突然将磁场撤去，那么经多少时间微粒到达Q点？（设PQ连线与电场方向平行）
如图所示，在x轴上方有垂直于xy平面向里的匀强磁场，磁感应强度为B；在x轴下方有沿y轴负方向的匀强电场，场强为E。一质量为m，电量为－q的粒子从坐标原点O沿着y轴正方向射出。射出以后，它第三次到达x轴时，与点O的距离为L。不计粒子重力，求：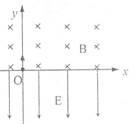
（1）粒子射出时的速度v；
（2）粒子从射出以后第三次到达x轴所用的总时间；
（3）若粒子从射出以后到第n次向下穿过x轴所用的总时间为tn，写出tn的表达式。
一带电粒子无初速度的进入一加速电场A，然后垂直进入两块平行金属板M、N形成的偏转电场中（偏转电场可视为匀强电场），如图所示。已知加速电场A板间电压为U1，M、N两板间的电压为U2，两板间的距离为d，板长为L，粒子的质量为m，电荷量为q，不计粒子受到的重力及它们之间的相互作用力。求：
（1）粒子穿过A板时速度大小v0；
（2）粒子从偏转电场射出时的侧移量y；
（3）粒子从偏转电场射出时速度的偏转角q。
如图所示，电源的总功率为40W，电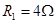阻
，
，电源内阻
，电源的输出功率为
。求：
（1）电源的内电路功率和电路中的总电流；
（2）电源的电动势；
（3）
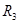的阻值。