如图，真空中有一匀强电场，方向沿Ox正方向，若质量为m、电荷量为q的带电微粒从O点以初速v0沿Oy方向进入电场，经Δt时间到达A点，此时速度大小也是vo，方向沿Ox轴正方向，如图所示。求：
从O点到A点的时间Δt。
该匀强电场的场强E及OA连线与Ox轴的夹角θ。
若设O点电势为零，则A点电势多大。
如图，匀强电场中有一半径为ｒ的光滑绝缘圆轨道，轨道平面与电场方向平行。ａ、b为轨道直径的两端，该直径与电场方向平行。一电荷为ｑ(q>０)的质点沿轨道内侧运动.经过a点和b点时对轨道压力的大小分别为Nａ和Ｎｂ不计重力，求电场强度的大小Ｅ、质点经过a点和b点时的动能。
一电荷量为q（q＞0）、质量为m的带电粒子在匀强电场的作用下，在t＝0时由静止开始运动，场强随时间变化的规律如图所示。不计重力，求在t＝0到t＝T的时间间隔内
（1）粒子位移的大小和方向；
（2）粒子沿初始电场反方向运动的时间。
半径为R，均匀带正电荷的球体在空间产生球对称的电场；场强火小沿半径分布如图所示，图中E0已知，E－r曲线下O－R部分的面积等于R－2R部分的面积。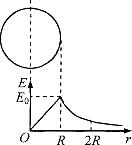
(1)写出E－r曲线下面积的单位；
(2)己知带电球在r≥R处的场强E＝kQ／r2，式中k为静电力常量，该均匀带电球所带的电荷量Q为多大?
(3)求球心与球表面间的电势差△U；
(4)质量为m，电荷量为q的负电荷在球面处需具有多大的速度可以刚好运动到2R处?
如图1所示，宽度为
的竖直狭长区域内（边界为
），存在垂直纸面向里的匀强磁场和竖直方向上的周期性变化的电场（如图2所示），电场强度的大小为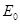
，
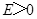表示电场方向竖直向上。
时，一带正电、质量为
的微粒从左边界上的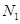
点以水平速度
射入该区域，沿直线运动到
点后，做一次完整的圆周运动，再沿直线运动到右边界上的
点。为线段
的中点，重力加速度为g。上述、、、、
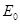为已知量。
(1)求微粒所带电荷量
和磁感应强度
的大小；
(2)求电场变化的周期
；
(3)改变宽度，使微粒仍能按上述运动过程通过相应宽度的区域，求的最小值。
如图所示，两平行金属板间距为d，电势差为U，板间电场可视为匀强电场；金属板下方有一磁感应强度为B的匀强磁场。带电量为+q、质量为m的粒子，由静止开始从正极板出发，经电场加速后射出，并进入磁场做匀速圆周运动。忽略重力的影响，求：
（1）匀强电场场强E的大小；
（2）粒子从电场射出时速度ν的大小；
（3）粒子在磁场中做匀速圆周运动的半径R。