如图所示,矩形单匝导线框abcd竖直放置,其下方有一磁感应强度为B的有界匀强磁场区域,该区域的上边界PP’水平,并与线框的ab边平行,磁场方向与线框平面垂直。已知线框ab边长为L1,ad边长为L2,线框质量为m,总电阻为R。现无初速地释放线框,在下落过程中线框所在平面始终与磁场垂直,且线框的ab边始终与PP’平行。重力加速度为g。若线框恰好匀速进入磁场,求:
dc边刚进入磁场时,线框受安培力的大小F
dc边刚进入磁场时,线框速度的大小v
在线框从开始下落到ab边刚进入磁场的过程中,重力做的功W
如图示,质量分别为m1、m2的两个物体通过轻弹簧连接,在力F作用下一起沿水平方向做匀速直线运动(m1在地面,m2在空中),力F与水平方向成θ角.求m1所受支持力N和摩擦力f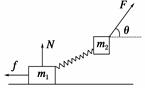
一物体沿直线运动,
(1)若它在前一半时间内的平均速度为v1,后一半时间的平均速度为v2,则全程的平均速度为多大?
(2)若它在前一半路程的平均速度为v1,后一半路程的平均速度为v2,则全程的平均速度为多大?
细绳一端系着质量M=8kg的物体,静止在水平面,另一端通过光滑小孔吊着质量m=2kg的物体,M的中点与圆孔的距离r=0.2m,已知M与水平面间的动摩擦因数为0.2,现使此物体M随转台绕中心轴转动,问转台角速度ω在什么范围m会处于静止状态?(g="10" m/s2)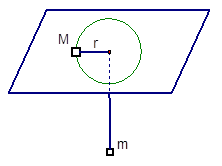
一个人从楼顶以20m/s的速度水平抛出一个小球,小球落到地面。小球在空中运动的水平位移为40m,不计空气阻力,重力加速度g取10m/s2。求:
(1)楼的高度h;
(2)小球落到地面时的速度v的大小;
(3)小球的抛出点与落地点之间的距离L。
2008年9月28日傍晚我国自行研制的“神舟”七号载人飞船经历68个多小时的太空飞行,在预定轨道绕地球飞行45圈后成功返回。设“神舟”七号载人飞船在圆轨道上绕地球运行n圈所用的时间为t,地球表面的重力加速度为g,地球半径为R,求:
(1)飞船的圆轨道离地面的高度;
(2)飞船在圆轨道上运行的速率。