如图，平面直角坐标系中，直线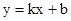
与x轴交于点A（2，0），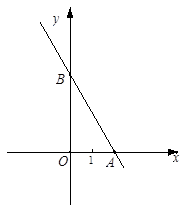
与y轴交于点B, 且tan∠BAO=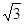
．（1）求直线的解析式；
（2）将直线
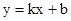绕点B旋转60°，求旋转后的直线解析式
(本题满分12分）
已知：⊙O的直径AB=8，⊙B与⊙O相交于点C、D，⊙O的直径CF与⊙B相交于点E，设⊙B的半径为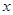
，OE的长为
。
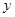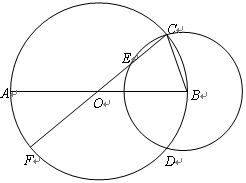
（1）如图，当点E在线段OC上时，求
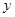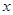关于的函数解析式，并写出定义域；（2）当点E在直径CF上时，如果OE的长为3，求公共弦CD的长；
（3）设⊙B与AB相交于G，试问△OEG能否为等腰三角形？如果能够，请直接写出BC弧的长度（不必写过程）；如果不能，请简要说明理由
（本小题满分12分）
某县有着丰富的海产品资源. 某海产品加工企业已收购某种海产品60吨, 根据市场信息, 如果对该海产品进行粗加工, 每天可加工8吨, 每吨可获利1000元；如果进行精加工, 每天可加工2吨, 每吨可获利5000元. 由于受设备条件的限制，两种加工方式不能同时进行.（1）设精加工的吨数为
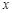吨, 则粗加工的吨数为 吨，加工这批海产品需要天, 可获利元(用含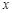的代数式表示)；（2）为了保鲜的需要, 该企业必须在两周(14天)内将这批海产品全部加工完毕，精加工的吨数
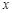在什么范围内时, 该企业加工这批海产品的获利不低于120000元?
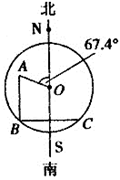
机器人“海宝”在某圆形区域表演“按指令行走”，如图所示，“海宝”从圆心O出发，先沿北偏西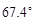
方向行走13m至A处，再沿正南方向行走14m至点B处，最后沿正东方向行走至点C处，点B、C都在圆O上。（1）求弦BC的长；
（2）求圆O的半径。（本题参考数据：
，
，
）
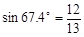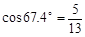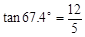已知关于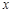
的一元二次方程
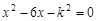（k为常数）（1）求证：方程有两个不相等的实数根。
（2）设
、
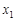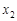为方程的两个实数根，且
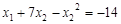试求k的值。
水是生命之源。长期以来，某市由于水价格不合理，一定程度上造成了水资源的浪费。为改善这一状况，相关部门正在研究制定居民用水价格调整方案。小明想为政府决策提供信息，于是在某小区内随机访问了部分居民，就每月的用水量、可承受的水价调整的幅度等进行调查，并把调查结果整理成图a、图b.
已知被调查居民每户每月的用水量在
之间，被调查的居民中对居民用水价格调价幅度抱“无所谓”态度的有8户，试回答下列问题：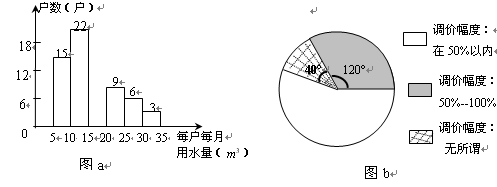
（1）图a使用的统计图表的名称是 ，它是表示一组数据 的量；（填“平均水平”、“离散程度”或“分布情况”）
（2）上述两个统计图表是否完整，若不完整，试把它们补全；
（3）若采用阶梯式累进制调价方案（如表1所示），试估计该小区有百分之几的居民用水费用的增长幅度不超过50%？
|
（含
）