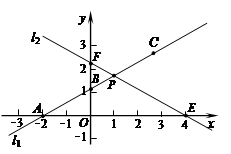如图，已知抛物线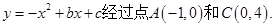
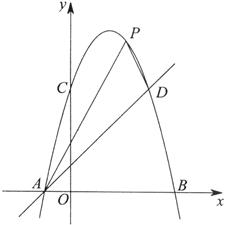
（1）求这条抛物线的解析式；
（2）
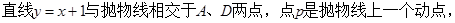点P的横坐标是m,且
值； （3）点M是直线AD上一动点，直线写出使△ACM为等腰三角形的点M的坐标．
有特大城市A及两个小城市B、C，这三个城市共建一个污水处理厂，使得该厂到B、C两城市的距离相等，且使A市到处理厂的管线最短，试确定污水处理厂的位置。（保留作图痕迹）
已知：如图，AB＝CD，DE⊥AC，BF⊥AC，E，
F是垂足，
．
求证：
．
如图，已知∠1=∠2，∠3=∠4，求证：△ABC≌△DCB
雨伞的中截面如图所示，伞骨AB=AC，支撑杆OE=OF，AE=
AB，AF=AC，当O沿AD滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD与∠CAD有何关系？说明理由。
在平面直角坐标系xOy中，已知直线l1经过点A(-2，0)和点B(0，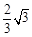
)，直线l2的函数表达式为
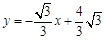，l1与l2相交于点P．⊙C是一个动圆，圆心C在直线l1上运动，设圆心C的横坐标是a．过点C作CM⊥x轴，垂足是点M．求直线l1的函数表达式；
当⊙C和直线l2相切时，请证明点P到直线CM的距离等于⊙C的半径R，并写出R=
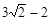时a的值.当⊙C和直线l2不相离时，已知⊙C的
半径R=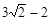，记四边形NMOB的面积为S(其中点N是直线CM与l2的交点)．S是否存在最大值？若存在，求出这个最大值及此时a的值；若不存在，请说明理由．
