如图，已知□ABCD中，AB=4，AD=2，E是AB边上的一动点（动点E与点A不重合，可与点B重合），设AE=
,DE的延长线交CB的延长线于点F，设CF=
，则下列图象能正确反映与的函数关系的是
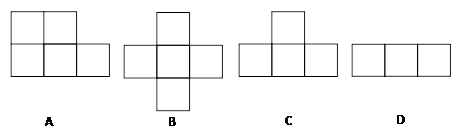
如图是一个由7个同样的立方体叠成的几何体.请问下列选项中，既是中心对称图形，又是这个几何体的三视图之一的是( )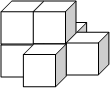
如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按逆时针方向旋转而得，则旋转的角度为（ ）
（A）30°（B）45°（C）90°（D）135°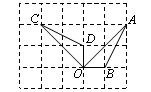
如果∠A为锐角，且sinA＝0.6，那么（ ）
Ａ．0°＜A＜30° B．30°＜A＜45°
Ｃ．45°＜A＜60°Ｄ．60°＜A＜90°
如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=3时，这两个二次函数的最大值之和等于【】
A．
B．
C．3 D．4
如图，△ABC是⊙O的内接三角形，AC是⊙O的直径，∠C=50°，∠ABC的平分线BD交⊙O于点D，则∠BAD的度数是【】
| A．45° | B．85° | C．90° | D．95° |