(本题10分)为了解八年级学生的课外阅读情况，我校语文组从八年级随机抽取了若干名学生，对他们的读书时间进行了调查并将收集的数据绘成了两幅不完整的统计图，请你依据图中提供的信息，解答下列问题：（每组含最小值不含最大值）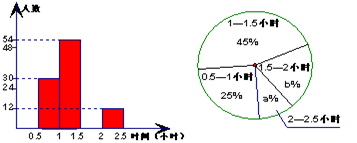
⑴从八年级抽取了多少名学生？
⑵填空 (直接把答案填到横线上)
①“2—2.5小时”的部分对应的扇形圆心角为_______度；
②课外阅读时间的中位数落在________(填时间段)内．⑶如果八年级共有800名学生，请估算八年级学生课外阅读时间
不少于1.5小时的有多少人？
如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同一时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上的影长为21米，留在墙上的影高为2米，求旗杆的高度.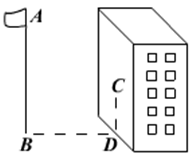
如图，△ACB和△ECD都是等腰直角三角形，∠ACB=∠ECD=90°，D为AB边上一点，
求证：（1）
；（2）
.
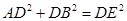将分别标有数字1，2，3 的三张卡片洗匀后，背面朝上放在桌面上.
（1）随机抽取一张，求抽到奇数的概率；
（2）随机抽取一张作为十位上的数字（不放回），再抽取一张作为个位上的数字，能组成哪些两位数？恰好是32的概率是多少.
某种电脑病毒传播非常快，如果一台电脑被感染，经过两轮感染后就会有81台电脑被感染．请你用学过的知识分析，每轮感染中平均一台电脑会感染几台电脑？若病毒得不到有效控制，3轮感染后，被感染的电脑会不会超过700台？
如图，已知一次函数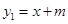
（m为常数）的图象与反比例函数
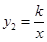（k为常数，
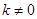）的图象相交于点 A（1，3）.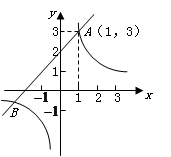
（1）求这两个函数的解析式及其图象的另一交点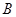
的坐标；
（2）观察图象，写出使函数值
的自变量
的取值范围.