(8分)在一个不透明的口袋里装有若干个相同的红球, 为了估计袋中红球的数量，某学习小组做了摸球实验, 他们将30个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色, 再把它放回袋中, 不断重复. 下表是几次活动汇总后统计的数据：（1） 请估计：当次数
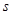很大时, 摸到白球的频率将会接近 ；假如你去摸一次, 你摸到红球的概率是 ；（精确到0.1）.（2） 试估算口袋中红球有多少只?
（3）解决了上面的问题后请你从统计与概率方面谈一条启示.
| 摸球的次数 |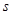
150 |
200 |
500 |
900 |
1000 |
1200 |
摸到白球的频数 |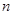
51 |
64 |
156 |
275 |
303 |
361 |
摸到白球的频率 |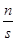
0.34 |
0.32 |
0.312 |
0.306 |
0.303 |
0.301 |
某自行车厂今年生产销售一种新型自行车，现向你提供以下有关信息：（1）该厂去年已备有这种自行车车轮10000只，车轮车间今年平均每月可生产车轮1500只，每辆自行车需装配2只车轮；（2）该厂装配车间（自行车最后一道工序的生产车间）每月至少可装配这种自行车1000辆，但不超过1200辆；（3）该厂已收到各地客户今年订购这种自行车共14500辆自行车的订货单；（4）这种自行车出厂销售单价为500元/辆。设该厂今年这种自行车的销售金额为a万元。请你根据上述信息，判断a的取值范围是多少？
某地区沙漠原有面积是100万公顷，为了解该地区沙漠面积的变化情况，进行连续3年的观察，并将每年年底的观察结果记录如下表。根据这些数据描点、连线，汇成曲线图，发现成直线状。
| 观察时间x |
该地区沙漠比原有面积增加数y |
| 第一年 |
0.2万公顷 |
| 第二年 |
0.4万公顷 |
| 第三年 |
0.6万公顷 |
预计该地区沙漠的面积将继续按此趋势扩大。
（1）如果不采取任何措施，那么到第m年底，该地区沙漠的面积将变成为＿＿万公顷。
（2）如果第五年底后，采取植树造林措施，每年改造0.8万公顷沙漠，那么到第几年底，该地区沙漠的面积能减少到95万公顷？
星期日早晨，小明的妈妈与单位的同事一同到客运公司乘坐旅游车外出旅游．妈妈出门片刻，小明发现妈妈将遮阳伞忘在家里，立即骑车去客运公司给妈妈送伞。车站停车场汽车云集，使人眼花缭乱，小明正为找不到妈妈乘坐的旅游车着急时，遇上了邻居王阿姨。王阿姨告诉他：你妈妈乘坐的那辆旅游车的牌照号码是个四位数，它的第一位数字与第二位数字相同，第三位数字与第四位数字相同，恰巧是一个完全平方数．亲爱的读者，你能帮小明找到这辆旅游车的牌照号码吗？
一客轮逆水行驶，船上一乘客掉了一件物品，浮在水面上，等乘客发现后，轮船立即掉头去追，已知轮船从掉头到追上共用5分钟，问乘客丢失了物品，是几分钟后发现的？
用直径为90mm的圆柱形玻璃杯（已装满水，且水足够多）向一个内底面积为131×131mm2，内高为81mm的长方体铁盒倒水，当铁盒装满水时，玻璃杯中水的高度下降了多少？（结果保留π）