如图所示,质量为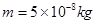 的带电粒子以
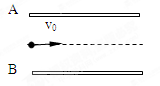
的带电粒子以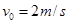 的速度从水平放置的平行金属板A、B中央飞入电场,已知板长L=10cm,板间距d=2cm,当AB间加电压
的速度从水平放置的平行金属板A、B中央飞入电场,已知板长L=10cm,板间距d=2cm,当AB间加电压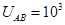 V时,带电粒子恰好沿直线穿过电场(设此时A板电
V时,带电粒子恰好沿直线穿过电场(设此时A板电 势高),重力加速度取g=10m/s2
势高),重力加速度取g=10m/s2
求:粒子带什么电?电荷量为多少?
A、B间所加电压为多少时,带电粒子刚好能从上极板右端飞出?
静电场方向平行于x轴,其电势φ随x的分布可简化为如图所示的折线,图中φ0和L为已知量。一个带负电的粒子在电场中以x=0为中心、沿x轴方向做周期性运动。已知该粒子质量为m、电荷量为-q,其动能与电势能之和为-E0(0<E0<qφ0)。忽略重力。求:
(1)粒子的运动区间;
(2)粒子的运动周期。
如图所示,水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接,半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×104 N/C。现有一电荷量q=+1.0×10-4C,质量m="0.10" kg的带电体(可视为质点),在水平轨道上的P点由静止释放,带电体运动到圆形轨道最低点B时的速度vB=5.0m/s。已知带电体与水平轨道间的动摩擦因数μ=0.50,重力加速度g=10m/s2。求:
(1)带电体运动到圆形轨道的最低点B时,圆形轨道对带电体支持力的大小;
(2)带电体在水平轨道上的释放点P到B点的距离L1;
(3)带电体第一次经过C点后,落在水平轨道上的位置到B点的距离L2。
如图所示的电路中,电源的电动势E=9V,内阻r=1Ω;电阻R1=10Ω,R2=10Ω,R3=30Ω,R4=40Ω;电容器的电容C=100μF,电容器原来不带电,求:
(1)开关S未接通时电源的电流I;
(2)接通开关S后流过R4的总电量Q。
质量为m=0.02kg通电细杆ab置于倾角为θ=370的平行放置的导轨上,导轨的宽度d=0.2m,杆ab与导轨间的动摩擦因数μ=0.4,磁感应强度B=2T的匀强磁场与导轨平面垂直且方向向下,调节滑动变阻器的滑片,让杆ab沿导轨匀速下滑。试求出通过杆ab的电流为多大。(g=10m/s2,sin370=0.6,cos370=0.8)
如图所示,在某市区,一辆小汽车在平直公路上向东匀速行驶,一位游客正由南向北从斑马线上匀速横穿马路,司机发现前方有危险(游客在D处),经0.7s作出反应,紧急刹车,仍将正步行至B处的游客撞伤,汽车最终停在C处,为了解现场,警方派一相同小车以法定最高速度vm=14m/s,行驶在同一路段,在肇事汽车的起始制动点A紧急刹车,经14m后停下来,现测得AB=17.5m、BC=14m、BD=2.6m,
问:(1)肇事汽车的初速度是多大?(2)游客横穿马路的速度是多大?