如图所示，在a、b两端有直流恒压电源，输出电压恒为Uab，R2=40Ω，右端连接间距d=0.04m、板长l=10cm的两水平放置的平行金属板，板间电场视为匀强电场。闭合开关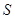
，将质量为m=1.6×10-6kg、带电量q=3.2×10-8C的微粒以初速度v0=0.5m/s沿两板中线水平射入板间。当滑动变阻器接入电路的阻值为15Ω时，微粒恰好沿中线匀速运动，通过电动机的电流为0.5A。已知电动机内阻R1=2Ω，取g=10m/s2。试问：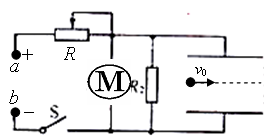
输出电压为Uab是多大？
在上述条件下，电动机的输出功率和电源的输出功率？
为使微粒不打在金属板上，R2两端的电压应满足什么条件？
如图乙所示，MN是一条通过透明球体球心的直线．在真空中波长为λ0=564nm的单色细光束AB平行于MN射向球体，B为入射点，若出射光线CD与MN的交点P到球心O的距离是球半径的
倍，且与MN所成的角α=30°．求：透明体的折射率；
一列简谐横波沿x轴正方向传播，在t=0时刻的波形如图甲所示，已知在t=1.1s时刻，质点P出现第三次波峰，求质点Q第一次出现波峰的时间。
如图所示，三物体用细绳相连，mA=1kg，mB=3kg，mC=1kg，A、C与水平桌面间的动摩擦因数
=0.25，求系统的加速度和AC绳中的张力。 
如图所示，飞机距地面高度为H，水平飞行速度v0，地面上停着一辆汽车，与飞机水平距离为X，欲使飞机投出炸弹击中汽车，H、v0、X应满足什么关系？(重力加速度为g)．
如图甲所示，一对足够长的平行光滑轨道放置在水平面上，两轨道相距L=1m，左端之间用R=3Ω的电阻连接，轨道的电阻忽略不计。一质量m=0.5kg、电阻r=1Ω的导体杆静置于两轨道上，并与两轨道垂直。整个装置处于磁感应强度B=2T的匀强磁场中，磁场方向垂直轨道平面向上。现用水平拉力沿轨道方向拉导体杆，拉力F与导体杆运动的位移x间的关系如图乙所示。当拉力达到最大时，导体杆恰好开始做匀速运动。当位移x=2.5m时撤去拉力，导体杆又滑行了一段距离△x后停下，已知在滑行△x的过程中电阻R上产生的焦耳热为12J。求：
（1）拉力F作用过程中，通过电阻R上的电量q；
（2）导体杆运动过程中的最大速度vm；
（3）拉力F作用过程中，回路中产生的焦耳热Q。