(本小题满分12分).
如图,已知某椭圆的焦点是F1(-4,0)、F2(4,0),过点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:|F2A|、|F2B|、|F2C|成等差数列.
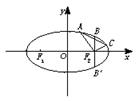
(1)求该弦椭圆的方程;
(2)求弦AC中点的横坐标;
(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.
已知圆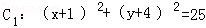 ,圆
,圆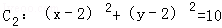 ,该两圆的交点为A,B两点,求:
,该两圆的交点为A,B两点,求:
(1)直线AB的方程
(2)A,B两点间的距离|AB|
(3)直线AB的垂直平分线的方程.
设函数y=f(x)是定义在(0,+∞)上的减函数,并且满足f(xy)=f(x)+f(y),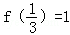 .
.
(1)求f(1)的值;
(2)如果f(x)+f(2﹣x)<2,求x的取值范围.
已知集合A={x|1≤x≤a},B={y|y=5x﹣6,x∈A},C={m|m=x2,x∈A}且B∩C=C,求a的取值范围.
已知函数f(x)=x2+2ax+2,x∈[﹣5,5],
(1)当a=1时,求f(x)的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[﹣5,5]上是单调函数.
已知M={1,2,a2﹣3a﹣1 },N={﹣1,a,3},M∩N={3},求实数a的值.