(13分)用磁场可以约束带电离子的轨迹,如图所示,宽d=2cm的有界匀强磁场的横向范围足够大,磁感应强度方向垂直纸面向里,B=1T。现有一束带正电的粒子从O点以v=2×106 m/s的速度沿纸面垂直边界进入磁场。粒子的电荷量q=1.6×10-19C,质量m=3.2×10-27kg。求:
(1)粒子在磁场中运动的轨道半径r和运动时间t是多大?
(2)粒子保持原有速度,又不从磁场上边界射出,则磁感应强度最小为多大?
如图所示的电路中,1、2、3、4、5、6为连接点的标号。在开关闭合后,发现小灯泡不亮。现用多用电表检查电路故障,需要检测的有:电源、开关、小灯泡、3根导线以及电路中的各点连接。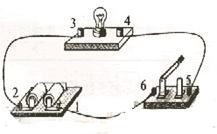
(1)为了检测小灯泡以及3根导线,在连接点1、2已接好的情况下,应当选用多用电表的挡。在连接点1、2同时断开的情况下,应当选用多用电表的挡。
(2)在开关闭合情况下,若测得5、6两点间的电压接近电源的电动势,则表明
可能有故障
(3)将小灯泡拆离电路,写出用多用表检测该小灯泡是否有故障的具体步骤。
如图所示,水平传送带上A、B两端点间 距L= 4m,半径R=1m的光滑半圆形轨道固定于竖直平面内,下端与传送带B相切。传送带以v0 = 4m/s的速度沿图示方向匀速运动,质量m =1kg的小滑块由静止放到传送带的A端,经一段时间运动到B端,滑块与传送带间的动摩擦因数μ = 0.5,取g=10m/s2。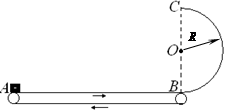
(1)求滑块到达B端的速度;
(2)求滑块由A运动到B的过程中,滑块与传送带间摩擦产生的热量;
(3)仅改变传送带的速度,其他条件不变,计算说明滑块能否通过圆轨道最高点C。
如图,一个质量为m的小球(可视为质点)以某一初速度从A点水平抛出,恰好从圆管BCD的B点沿切线方向进入圆弧,经BCD从圆管的最高点D射出,恰好又落到B点.已知圆弧的半径为R且A与D在同一水平线上,BC弧对应的圆心角θ=60°,不计空气阻力.求: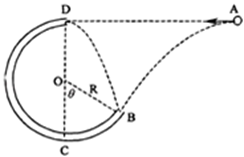
(1)小球从A点做平抛运动的初速度v0的大小;
(2)在D点处管壁对小球的作用力N;
(3)小球在圆管中运动时克服阻力做的功Wf.
所受重力G1="8" N的砝码悬挂在绳PA和PB的结点上.PA偏离竖直方向37°角,PB在水平方向,且连在所受重力为G2="100" N的木块上,木块静止于倾角为37°的斜面上,如图所示,试求: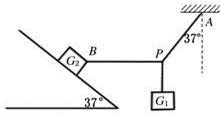
(1)木块与斜面间的摩擦力
(2)木块所受斜面的弹力
科技的发展给人们生活带来了极大的方便,荆州火车站从2012年7月1日开通运营后不久,“和谐号”动车D5714便投入运营,大大缩短了人们出行时间。D5714在早上8点24分从荆州出发途经仙桃西、天门南、汉川,10点14分到达终点站武昌火车站,其中在仙桃西、天门南、汉川每站停留两分钟,设动车出站和进站时做匀变速直线运动且加速度大小相等,从减速到进站需要5分钟,全程平均时速为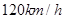 ,最高时速为
,最高时速为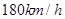 ,设动车启动达到最高时速后一直以该速度匀速行驶直到下一站减速进站停止,试求:
,设动车启动达到最高时速后一直以该速度匀速行驶直到下一站减速进站停止,试求:
(1)荆州到武昌的路程有多远?出站加速度是多少
(2)动车因停靠各站所耽搁的时间是多少分多少秒