设抛物线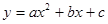
与X轴交于两不同的点
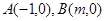(点A在点B的左边)，与y轴的交点为点C(0,-2)，且∠ACB=900．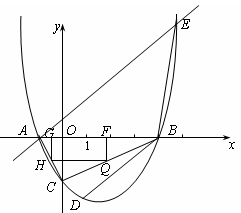
（1）求m的值和该抛物线的解析式；
（2）若点D为该抛物线上的一点，且横坐标为1，点E为过A点的直线y=x+1与该抛物线的另一交点.在X轴上是否存在点P，使得以P、B、D为顶点的三角形与△AEB相似，若存在，求出点P的坐标，若不存在，请说明理由．
（3）连结AC、BC，矩形FGHQ的一边FG在线段AB上，顶点H、Q分别在线段AC、BC上，若设F点坐标为（t，0），矩形FGHQ的面积为S，当S取最大值时，连接FH并延长至点M，使HM=k·FH，若点M不在该抛物线上，求k的取值范围．
在一个不透明的袋中装有除颜色外其余均相同的n个小球，其中有5个黑球，从袋中随机摸出一球，记下其颜色，这称为一次摸球试验，之后把它放回袋中，搅匀后，再继续摸出一球，以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表：
| 摸球试验次数 |
100 |
1000 |
5000 |
10000 |
50000 |
100000 |
| 摸出黑球次数 |
46 |
487 |
2506 |
5008 |
24996 |
50007 |
根据列表，可以估计出n的值是 ．
如图，已知点A（0，1），B（0，-1），以点A为圆心，AB为半径作圆，交x轴的正半轴于点C，则∠BAC等于 度．
如果一个正多边形的中心角为45°，那么这个正多边形的边数是 ．
将点（0，0），（5，4），（3，0），（5，1），（5，﹣1），（3，0），（4，﹣2），（0，0），在上面坐标系A中描出，并顺次连接画在A中．（对以下问题请将图形代码填入相应的括号内）做如下变化：
（1）横坐标保持不变，纵坐标分别乘以﹣1，再将所得的点用线段依次连接起来，所得的图案是 ；
（2）纵坐标保持不变，横坐标分别变为原来的2倍，再将所得的 点用线段依次连接起来，所得的图案是 ；
（3）纵坐标保持不变，横坐标分别加3，再将所得的 点用线段依次连接起来，所得的图案是 ．
某机动车出发前油箱内有油42L，行驶若干小时后，途中在加油站加油若干升，油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据图回答问题：
（1）机动车行驶 h后加油；
（2）加油前油箱余油量Q与行驶时间t的函数关系式是 ；
（3）中途加油 L；
（4）如果加油站距目的地还有230km，车速为40km/h，要到达目的地，油箱中的油是否够用？请说明理由．