设函数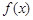 是定义在
是定义在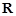 上的奇函数,且当
上的奇函数,且当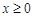 时,
时,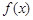 单调递减,若数列
单调递减,若数列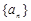 是等差数列,且
是等差数列,且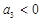 ,则
,则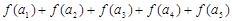 的值
的值
| A.恒为0 | B.恒为负数 | C.恒为正数 | D.可正可负 |
为得到函数 的图象, 只需要将函数
的图象, 只需要将函数 的图象向( ) 个单位
的图象向( ) 个单位
A.左平移 |
B.右平移 |
C.左平移 |
D.右平移 |
下面的程序框图,如果输入三个实数a、b、c,要求输出这三个数中最大的数,
那么在空白的判断框中,应该填入下面四个选项中的是 
| A.c > x | B.x > c | C.c > b | D.b > c |
对变量x, y 有观测数据( ,
, )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1图2
| A.变量x 与y 正相关,u 与v 正相关 |
| B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 |
| D.变量x 与y 负相关,u 与v 负相关 |
若方程 表示的曲线为圆,则
表示的曲线为圆,则 的取值范围是()
的取值范围是()
A.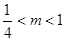 |
B. . . |
C. |
D. |
已知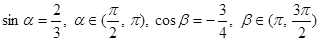 ,则
,则
A. |
B.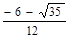 |
C. |
D. |