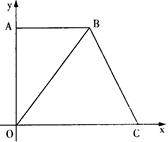
如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A在y轴上，点C在x轴上，且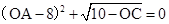
，OB＝OC．求点B的坐标；
点P从C点出发，沿线段CO以5个单位/秒的速度向终点O匀速运动，过点P作PH⊥OB，垂足为H，设△HBP的面积为S（S≠0），点P的运动时间为t秒，求S与t之间的函数关系式（直接写出自变量t的取值范围）；
在（2）的条件下，过点P作PM∥CB交线段AB于点M，过点M作MR⊥OC，垂足为R，线段MR分别交直线PH、OB于点E、G，点F为线段PM的中点，联结EF．
①判断EF与PM的位置关系；
②当t为何值时，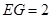
？
（本题7分）已知：a，b，c为△ABC的三边长，且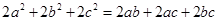
，试判断△ABC的形状，并证明你的结论．
（本题6分）△ABC在平面直角坐标系中的位置如图所示．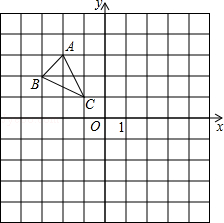
（1）作出△ABC关于y轴对称的三角形△A1B1C1；
（2）将△A1B1C1向下平移3个单位长度，画出平移后的△A2B2C2．
（本题6分）先化简，再求值：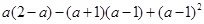
，其中
的绝对值等于1．
（每题4分，共8分）因式分解：
（1）
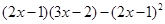
（2）
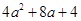
拖拉机在行驶的过程中的噪音会影响周围环境，某拖拉机位于A学校正南方向130m的B处，正以120m/min的速度沿公路BC方向行驶，如图所示，已知A学校到BC的距离AD=50m，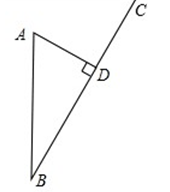
（1）求拖拉机从B处行驶到D处经过多长时间？
（2）如果在距拖拉机100m的圆形区域内都将受噪音影响，那么A学校受到拖拉机噪音影响的时间有多长？（结果精确到0.1，
≈1.732）