(本题满分10分) (1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′ 处(如图1),折痕为EF.小明发现△ AEF为等腰三角形,你同意吗?请说明理由.(3分)

(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.(4+3分)

列代数式:
(1)把a本书平均分给若干名学生,若每人分5本,还余3本,则学生人数为________;
(2)若圆A的半径r是圆B的半径的5倍,则这两个圆的周长之和为________;
(3)如图所示是由形状相同的正六边形和正三角形镶嵌而成的一组有规律的图案,则第n个图案中阴影小三角形的个数是________(用含n的代数式表示).
先观察下列等式,再回答下列问题.
① ;
;
②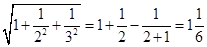 ;
;
③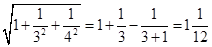 ;
;
……
(1)根据上面三个等式提供的信息,试猜想 的结果是什么.
的结果是什么.
(2)请按照上面各式反映的规律,写出用n(n为正整数)表示的等式.
甲同学和乙同学做一道相同的题目“先化简,再求值: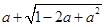 ,其中a=9”时得出了不同的答案.
,其中a=9”时得出了不同的答案.
甲同学的做法是:原式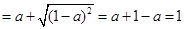 .
.
乙同学的做法是:因为a=9,所以a-1>0,所以原式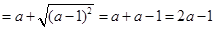 ,当a=9时,
,当a=9时,
原式=2×9-1=17.
到底谁做错了?为什么?
(1)把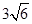 ,
,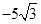 中根号外的数适当改变后,移到根号里面;
中根号外的数适当改变后,移到根号里面;
(2)你能将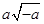 中根号外的因式适当改变后,移到根号里面吗?
中根号外的因式适当改变后,移到根号里面吗?
如图,若观测点的高度为h,观测者视线能达到的最远距离为d,则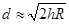 ,其中R是地球半径(通常取6400km).
,其中R是地球半径(通常取6400km).
(1)小丽站在海边一块岩石上,眼睛离地面的高度为20m,此时小丽视线能达到的最远距离为多少千米?
(2)已知泰山到海边的最近距离是216000m,泰山的海拔高度为1545m,利用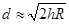 计算,判断站在泰山之巅能否看到大海.
计算,判断站在泰山之巅能否看到大海.