如图, 正方形ABCO放在平面直角坐标系中,其中点O为坐标原点,A、 C两点分别在x 轴的负半轴和y轴的正半轴上,点B的坐标为(-4,4)。已知点E、点F分别从A、点B同时出发,点E以每秒2个单位长度的速度在线段AB上来回运动. 点F沿B→C→0方向,以每秒1个单位长度的速度向点O运动.,当点F到达点O时,E、F两点都停止运动.在E、F的运动过程中,存在某个时刻,使得△OEF的面积为6.那么点E的坐标为 。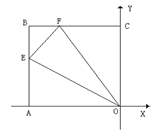
如图所示的各图表示由若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数为s,按此规律推断,以s,n为未知数的二元一次方程为s= .
解方程组 时,甲正确解出
时,甲正确解出 ,乙因看错了c,而求得
,乙因看错了c,而求得 ,则a,b,c的值分别为 , , .
,则a,b,c的值分别为 , , .
对于数x、y,定义一种新的运算*,x*y=ax+by,其中a,b为常数,等式的右边是通常的加法与乘法运算.已知3*5=15,4*7=28,则1*1= .
小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图所示,请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是 cm.
2008年北京第29届奥运会,中国,美国,俄罗斯获得奖牌总数分别是100,110,72,其中中国和俄罗斯的银牌、铜牌总数分别相等,俄罗斯的金牌总数比中国的金牌总数少28枚,而美国金牌总数比俄罗斯多13枚,美国的金牌总数与铜牌总数相等,银牌总数比金牌总数多2枚.中国的铜牌总数比银牌总数多7枚.请你根据上述信息计算一下中国的金牌总数是 ,美国的银牌总数是 ,俄罗斯的铜牌总数是 .