结合数轴与绝对值的知识回答下列问题:
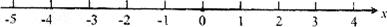
数轴上表示1和4的两点之间的距离是_________;表示-3和2的两点之间的距离是_________;表示-5和-4的两点之间的距离是_________;一般地,数轴上表示数
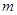 和数
和数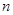 的两点之间的距离等于_____________.
的两点之间的距离等于_____________.
如果表示数
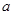 和-2的两点之间的距离是3,那么
和-2的两点之间的距离是3,那么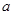 =__________.
=__________.
若数轴上表示数
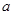 的点位于-4与2之间,求
的点位于-4与2之间,求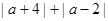 的值;
的值;
当
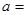 ______时,
______时,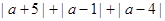 的值最小,最小值是____________
的值最小,最小值是____________
我市某工艺厂为配合奥运会,设计了一款成本为20元∕件的工艺品投放市场进行试销.经过调查,得到如下数据:
| 销售单价x(元/件) |
…… |
30 |
40 |
50 |
60 |
…… |
| 每天销售量y(件) |
…… |
500 |
400 |
300 |
200 |
…… |
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式; 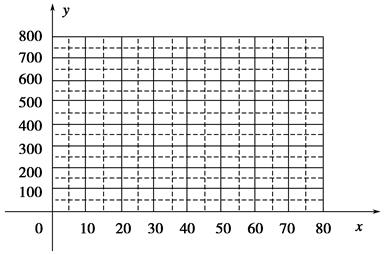
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?(利润=销售总价-成本总价)
(3)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?
如图,阅读对话,解答问题.
(1)试用树形图或列表法写出满足关于x的方程x2+px+q=0的所有等可能结果;
(2)求(1)中方程有实数根的概率.
先阅读下列材料,然后解答问题:
材料1 从3张不同的卡片中选取2张排成一列,有6种不同的排法,抽象成数学问题就是从3个不同元素中选取2个元素的排列,排列数记为A32=3×2=6.
一般地,从n个不同元素中选取m个元素的排列数记作Anm,
Anm=n(n-1)(n-2)…(n-m+1)(m≤n).
例:从5个不同元素中选3个元素排成一列的排列数为:A53=5×4×3=60.
材料2 从3张不同的卡片中选取2张,有3种不同的选法,抽象成数学问题就是从3个元素中选取2个元素的组合,组合数记为C32= =3.
=3.
一般地,从n个不同元素中选取m个元素的组合数记作Cnm,
Cnm=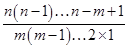 (m≤n).
(m≤n).
例:从6个不同元素中选3个元素的组合数为:
C63= =20.
=20.
问:(1)从7个人中选取4人排成一排,有多少种不同的排法?
(2)从某个学习小组8人中选取3人参加活动,有多少种不同的选法?
阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2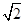 =(1+
=(1+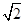 )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b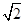 =(m+n
=(m+n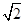 )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b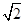 =m2+2n2+2mn
=m2+2n2+2mn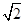 .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b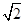 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n
=(m+n )2,用含m、n的式子分别表示a、b,得a=________,b=________;
)2,用含m、n的式子分别表示a、b,得a=________,b=________;
(2)利用所探索的结论,找一组正整数a、b、m、n,填空:________+________ =(______+______
=(______+______ )2;
)2;
(3)若a+4 =(m+n
=(m+n )2,且a、m、n均为正整数,求a的值.
)2,且a、m、n均为正整数,求a的值.
如图,正方形ABCD和正方形EFGH的边长分别为2和,对角线BD、FH都在直线L上,O1、O2分别是正方形的中心,线段O1O2的长叫做两个正方形的中心距。当中心O2在直线L上平移时,正方形EFGH也随平移,在平移时正方形EFGH的形状、大小没有改变.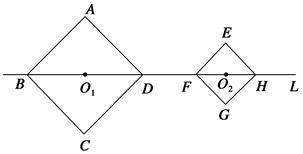
(1)计算:O1D=________,O2F=________.
(2)当中心O2在直线L上平移到两个正方形只有一个公共点时,中心距O1O2=________.
(3)随着中心O2在直线L上的平移,两个正方形的公共点的个数还有哪些变化?并求出相对应的中心距的值或取值范围(不必写出计算过程).