探究题：先观察下列等式，再回答问题①；②；③；④你判断完以上-优题课

探究题：先观察下列等式，再回答问题
①； ②；
③； ④
你判断完以上各题之后，发现了什么规律？请用含有n的式子将规律表示出来，并注明n的取值范围
请用数学知识说明你所写式子的正确性．

科目数学题型解答题难度中等

知识点：二元二次方程组

如图， $AB$ 为 $⊙ O$ 的直径，点 $C$ 为 $⊙ O$ 上一点，将弧 $BC$ 沿直线 $BC$ 翻折，使弧 $BC$ 的中点 $D$ 恰好与圆心 $O$ 重合，连接 $OC$ ， $CD$ ， $BD$ ，过点 $C$ 的切线与线段 $BA$ 的延长线交于点 $P$ ，连接 $AD$ ，在 $PB$ 的另一侧作 $∠ MPB = ∠ ADC$ ．

（1）判断 $PM$ 与 $⊙ O$ 的位置关系，并说明理由；

（2）若 $PC = \sqrt{3}$ ，求四边形 $OCDB$ 的面积．

数学课上，李老师准备了四张背面看上去无差别的卡片 $A$ ， $B$ ， $C$ ， $D$ ，每张卡片的正面标有字母 $a$ ， $b$ ， $c$ 表示三条线段（如图），把四张卡片背面朝上放在桌面上，李老师从这四张卡片中随机抽取一张卡片后不放回，再随机抽取一张．

（1）用树状图或者列表表示所有可能出现的结果；

（2）求抽取的两张卡片中每张卡片上的三条线段都能组成三角形的概率．

某公司计划购买 $A$ ， $B$ 两种型号的电脑，已知购买一台 $A$ 型电脑需0.6万元，购买一台 $B$ 型电脑需0.4万元，该公司准备投入资金 $y$ 万元，全部用于购进35台这两种型号的电脑，设购进 $A$ 型电脑 $x$ 台．

（1）求 $y$ 关于 $x$ 的函数解析式；

（2）若购进 $B$ 型电脑的数量不超过 $A$ 型电脑数量的2倍，则该公司至少需要投入资金多少万元？

某初级中学数学兴趣小组为了了解本校学生的年龄情况，随机调查了该校部分学生的年龄，整理数据并绘制如下不完整的统计图．

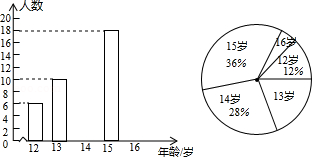
依据以上信息解答以下问题：

（1）求样本容量；

（2）直接写出样本的平均数，众数和中位数；

（3）若该校一共有1800名学生，估计该校年龄在15岁及以上的学生人数．

甲乙两人做某种机械零件，已知甲每小时比乙多做4个，甲做120个所用的时间与乙做100个所用的时间相等，求甲乙两人每小时各做几个零件？

试卷网试题网古诗词网作文网范文网