某商场购进一种单价为40元的篮球,如果以单价50元售出,那么每月可售出500个,根据销售经验,销售单价每提高1元,销售量相应减少10个设销售单价提高x元(x为正整数),写出每月销售量y(个)与x(元)之间的函数关系式;
假设这种篮球每月的销售利润为w元,试写出w与x之间的函数关系式,并通过配方讨论,当销售单价定为多少元时,每月销售这种篮球的利润最大,最大利润为多少元?
已知 ,求
,求 的值.
的值.
解分式方程: .
.
如图,∠AOB="90°," OA=OB,,直线EF经过点O,AC⊥EF与点C,BD⊥EF与点D,求证:AC=OD.
设p,q都是实数,且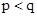 .我们规定:满足不等式
.我们规定:满足不等式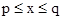 的实数x的所有取值的全体叫做闭区间,表示为
的实数x的所有取值的全体叫做闭区间,表示为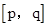 .对于一个函数,如果它的自变量x与函数值y满足:当
.对于一个函数,如果它的自变量x与函数值y满足:当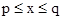 时,有
时,有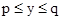 ,我们就称此函数是闭区间
,我们就称此函数是闭区间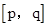 上的“闭函数”.
上的“闭函数”.
(1)反比例函数 是闭区间
是闭区间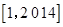 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数 是闭区间
是闭区间 上的“闭函数”,求此函数的解析式;
上的“闭函数”,求此函数的解析式;
(3)若实数c,d满足 ,且
,且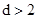 ,当二次函数
,当二次函数 是闭区间
是闭区间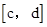 上的“闭函数”时,求c,d的值.
上的“闭函数”时,求c,d的值.
已知:如图,△MNQ中,MQ≠NQ.
(1)请你以MN为一边,在MN的同侧构造一个与△MNQ全等的三角形,画出图形,并简要说明构造的方法;
(2)参考(1)中构造全等三角形的方法解决下面问题:
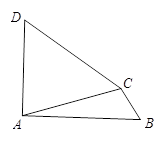
如图,在四边形ABCD中,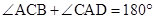 ,∠B=∠D.求证:CD=AB.
,∠B=∠D.求证:CD=AB.