已知:如图①,在 中,
中, ,
,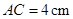 ,
,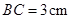 ,点
,点 由
由 出发沿
出发沿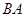 方向向点
方向向点 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点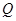 由
由 出发沿
出发沿 方向向点
方向向点 匀速运动,速度为2cm/s;连接
匀速运动,速度为2cm/s;连接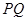 .若设运动的时间为
.若设运动的时间为 (
( ),解答下列问题
),解答下列问题
当
 为何值时,
为何值时, ?
?设
 的面积为
的面积为 (
(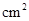 ),求
),求 与
与 之间的函数关系式;
之间的函数关系式;是否存在某一时刻
 ,使线段
,使线段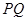 恰好把
恰好把 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时 的值;若不存在,说明理由;
的值;若不存在,说明理由;如图②,连接
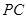 ,并把
,并把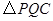 沿
沿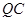 翻折,得到四边形
翻折,得到四边形 ,那么是否存在某一时刻
,那么是否存在某一时刻 ,使四边形
,使四边形 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
某中学为了了解全校的耗电情况,抽查了某月(30天)中全校每天的耗电量,数据如右表:
| x(度数) |
90≤x<100 |
100≤x<110 |
110≤x<120 |
120≤x |
| 天数 |
5 |
6 |
12 |
7 |
| 百分数 |
17% |
20% |
40% |
23% |
(1)耗电量的中位数所在组的范围是___________________。
(2)根据数据绘制你认为恰当的统计图。
已知某直线经过(3,5),(-4,-9)两点,求该直线的函数解析式。
化简: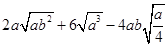
计算: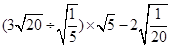
在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N .
(1)写出点C的坐标;
(2)求证:MD = MN;
(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明.
