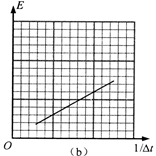
在“研究回路中感应电动势大小与磁通量变化快慢的关系”实验中，得到E－1/Δt图线如图所示。
从观察和分析该实验装置可看出，在实验中，因磁铁相对螺线管位置的变化都 （选填“相同”或“不同”），从而实现了控制 不变。
在得到实验数据之后，为了研究E与Δt的关系，可采用图像处理数据的方法，在直角坐标系中作E－1/Δt的关系图线，由图像可得出的实验结论是 ________________________________。
仅将线圈匝数变为原来3倍后重新做实验，在E－1/Δt画出实验图线。
（I）为了探究“感应电流产生的条件”，甲同学将电池组、滑线变阻器、带铁芯的线圈A、线圈B、电流计及开关如图连接. 经乙同学检查后发现甲同学接线有错误，应该导线是 _________（用导线两端的字母符号表示）。如果在闭合电键时发现灵敏电流计的指针向右偏了一下，那么合上电键后可能出现的情况有：将原线圈迅速插入副线圈时，灵敏电流计指针将________。（填“向右偏”、“向左偏”或“不偏转”）原线圈插入副线圈后，将滑动变阻器触头迅速向左拉时，灵敏电流计指针___________。（填“向右偏”、“向左偏”或“不偏转”）
某探究学习小组的同学欲以如图装置中的滑块为对象验证“动能定理”，他们在实验室组装了一套如图所示的装置，另外他们还找到了打点计时器所用的学生电源、导线、复写纸、纸带、小木块、细沙、垫块等需要的东西。当滑块连接上纸带，用细线通过滑轮挂上空的小沙桶时，释放小桶，滑块处于静止状态。若你是小组中的一位成员，要完成该项实验，则：
（1）实验时为了保证滑块（质量为
）受到的合力与沙和沙桶的总重力大小基本相等，实验时首先要做的步骤是 ，另外沙和沙桶的总质量
应满足的实验条件是 。
（2）在（1）的基础上，某同学用天平称量滑块的质量。往沙桶中装入适量的细沙，用天平称出此时沙和沙桶的总质量。让沙桶带动滑块加速运动，用打点计时器记录其运动情况，在打点计时器打出的纸带上取两点，测出这两点的间距L和这两点的速度大小
与
（< ）。则对滑块，本实验最终要验证的数学表达式为 （用题中的字母表示）。
（3）由于实验原理上的原因，上述数学表达式只能是近似成立，那么，此试验中真正成立的等式为 （仍用上述题中的字母表示）。
同学用电阻箱、多用电表、开关和导线测一节旧干电池的电动势和内阻．
（1）他先用多用表电压档直接接在电源两极，读数如图甲，则电源电动势约为 V．
（2）为了更准确的测量电源的电动势和内电阻，他用多用表的“直流100mA”档设计了如图乙的测量电路，为了电表安全，请估算开关闭合前电阻箱的最小取值为 Ω．
（3）将多用电表的选择开关从OFF旋转至“直流100mA”档，调节电阻箱到合适的值并记录其读数R，合上开关从多用表上读出相应的示数I．
（4）重复（3）获得多组数据，根据数据作出了如图丙所示的
图线．
（5）由图线得干电池的电动势E= V（保留三位有效数字），内阻r= Ω（取整数），多用表的内电阻对 （选填“E”、“r”或“E和r”）的测量结果有影响．
【改编】在用接在50Hz交流电源上的打点计时器测定小车做匀加速直线运动的加速度的实验中，得到如图甲所示的一条纸带，从比较清晰的点开始标计数点0、1、2、3、4，其中每两个计数点间还有4个点未画出，量得0与1两计数点间的距离x1=20mm，3与4两计数点间的距离x4=50mm，1与3两计数点间的距离 m，小车的加速度为______m/s2。
某同学要测定一电的电动势E和内电阻r，实验器材有：一只DIS电流传感器（可视为理想电流表，测得的电流用I表示），一只电阻箱（阻值用R表示），一只开关和导线若干。该同学设计了如图甲所示的电路进行实验和采集数据．
（1）该同学设计该实验的原理表达式是__________________（用E、r、I、R表示）；
（2）该同学在闭合开关之前，应先将电阻箱阻值调至________（选填“最大值”、“最小值”或“任意值”），在实验过程中，将电阻箱调至图乙所示位置，则此时电阻箱接入电路的阻值为________Ω；
（3）该同学根据实验采集到的数据做作出如图丙所示的
图象，则由图象求得，该电的电动势E=________V，内阻r=________Ω（结果均保留两位有效数字）。