,7分)计算: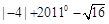
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,AB=a.
(1)求∠ABC的度数.
(2)求对角线AC的长度.
(3)求菱形ABCD的面积.
如图,已知正方形ABCD的边长为1,连接AC、BD,CE平分∠ACD交BD于点E,求DE的长.
如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.
(1)求∠ABD的度数;
(2)求线段BE的长.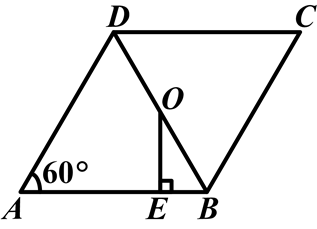
在Rt△ABC中,∠ACB=90°,AB=2AC,如图所示,求∠A、∠B的度数.
把长与宽之比为 的矩形纸片称为标准纸,请思考并解决下列问题:
的矩形纸片称为标准纸,请思考并解决下列问题:
(1)将一张标准纸ABCD(AB<BC)对开,如图1所示,所得的矩形纸片ABEF是标准纸,请给予证明;
(2)在一次综合实践课上,小明尝试着将矩形纸片ABCD(AB<BC)进行如下操作:
第一步:沿过A点的直线折叠,使B点落在AD边上点F处,折痕为AE(如图2甲);
第二步:沿过D点的直线折叠,使C点落在AD边上点N处,折痕为DG(如图2乙),此时E点恰好落在AE边上的点M处;
第三步:沿直线DM折叠(如图2丙),此时点G恰好与N点重合.
请你探究:矩形纸片ABCD是否是一张标准纸,请说明理由;
(3)不难发现:将一张标准纸按如图3所示方式一次又一次对开后,所得的矩形纸片都是标准纸,现有一张标准纸ABCD,AB=1, ,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2014次对开后所得标准纸的周长.
,问第5次对开后所得标准纸的周长是多少?探索并直接写出第2014次对开后所得标准纸的周长.